共计 1028 个字符，预计需要花费 3 分钟才能阅读完成。

在研究性文章中，我们经常会看到“P值”。

但P值究竟是什么，它又如何影响我们的研究结论呢？

今天，我们就来一起聊一聊这个“P值”。

什么是P值？

P值（P-value）是统计学中用于假设检验的一个关键概念。它的定义是：

在原假设  成立的条件下，检验统计量  出现给定观测值或者比之更极端值的概率。

“直观上,用以描述抽样结果与理论假设的吻合程度，因而也称 P值为拟合优度。

例如，正态总体参数检验 （原假设），（备择假设） 的情况下，

检验统计量为 ，即由样本数据得到的检验统计量  的观测值为 ，则P值为

P值的特点：

1. 范围：P值的范围在0到1之间。
2. 计算：通过统计检验（如t检验、卡方检验、ANOVA等）计算得出。
3. 解释：
   • 小P值：如果P值很小（通常小于0.05），则认为观测数据在原假设为真的条件下出现的可能性很小，因此我们有足够的证据拒绝原假设，接受备择假设。
   • 大P值：如果P值较大（通常大于0.05），则没有足够的证据拒绝原假设。
4. 阈值：研究者会设定一个显著性水平（），如0.05，作为判断是否拒绝原假设的标准。
5. 误解：P值并不表示备择假设为真的概率，也不表示效应的大小或效应的实际意义。

如何使用P值？

假设检验中，P值检验法的原则是当  值小到一定程度时拒绝 。

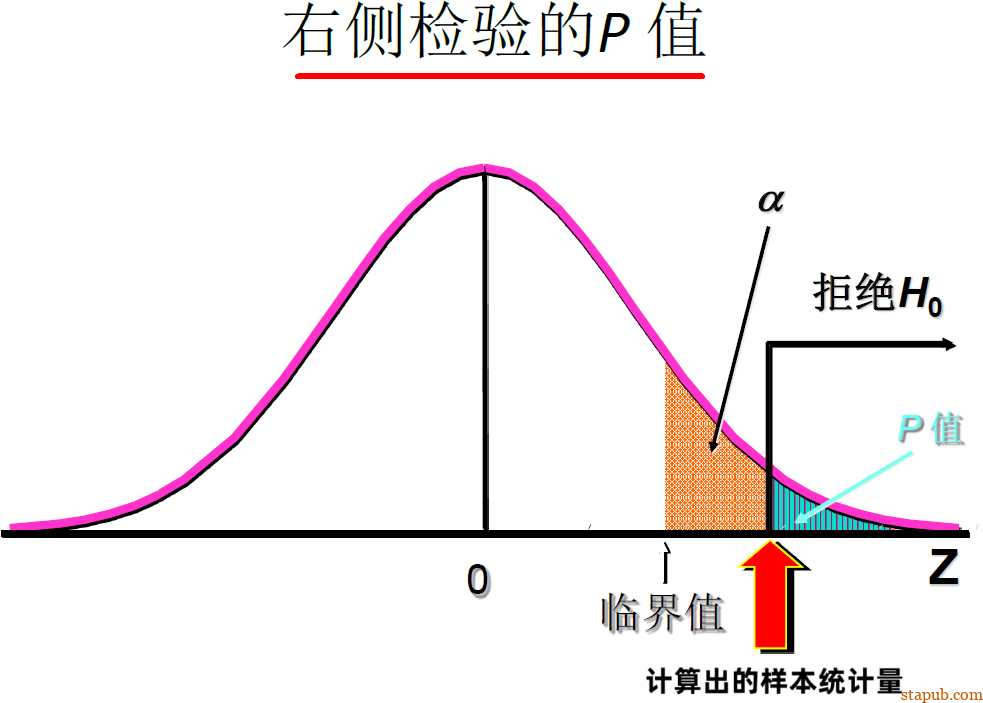
如下图所示，

1. 如果  ，即检验统计量  的观测值  在拒绝域内，则在显著性水平  下拒绝原假设 。
2. 如果 ，则在显著性水平  下接受原假设 。

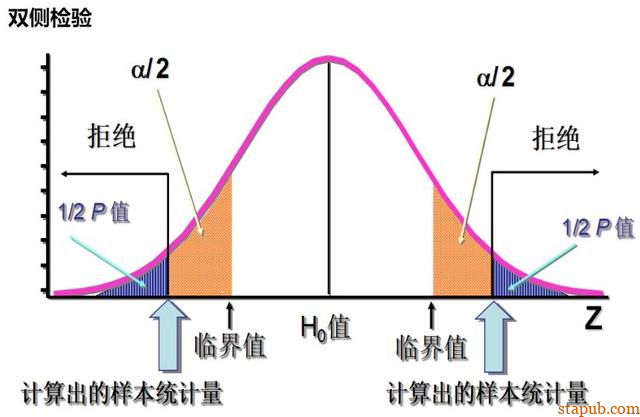
“通常约定： 称结果为显著； 则称结果为高度显著。

例如，一家汽车厂商声称他们生成的节能型汽车的耗油量低于29（单位：英里/加仑，简称mpg）。

但是，另一家汽车厂商对这个数据表示怀疑，于是他调查了一组同型号的汽车的行驶记录共计16条，得到了这个型号汽车平均耗油量观测值为28。（假设该节能型汽车的耗油量服从正态分布 。）

请问，在显著性水平  假定下，能否接受耗油量低于29的假设？如果显著性水平为 ，则结论会有变化吗？

解：首先，建立假设:（原假设），（备择假设）；

其次，给出未知参数  的估计值 ;

然后，计算 值：

“通常，P值的计算可以通过统计软件（如SPSS、R、SAS等）自动完成，或者通过查阅相应的统计表来手动计算。

最后，解释P值：

• 当显著性水平  时，，故不能拒绝 ，认为耗油量不低于；
• 当显著性水平  时，，故拒绝，认为耗油量低于。

结语

P值是统计推断中一个非常有用的工具，但它的解释和使用需要谨慎，以避免误解和错误的结论。

理解P值，让数据分析更科学！