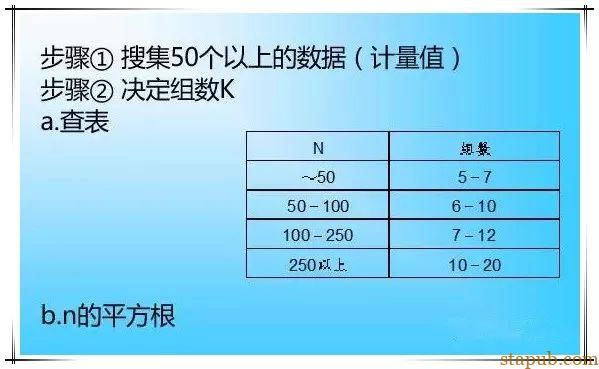
共计 2874 个字符,预计需要花费 8 分钟才能阅读完成。
1953年石用馨教授所提出的一种以把握结果(特性)与原因(要因)的极方便而有效的方法。特性要因图就是能一目了然的表示出结果(制品的特性)与在(影响特性的要因)之影响情形或二者之间的关系之图形。因其形状很像鱼骨,故又称为“鱼骨图”。
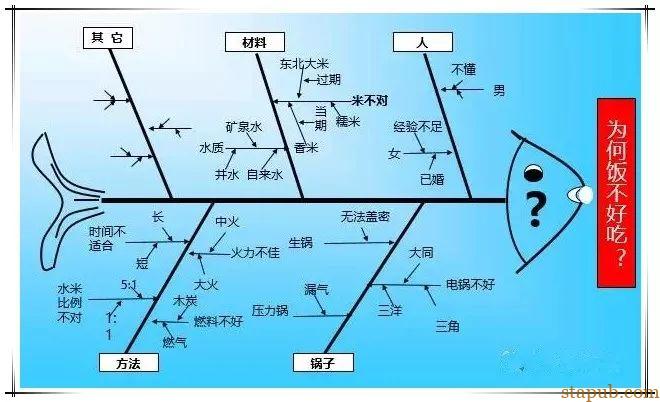
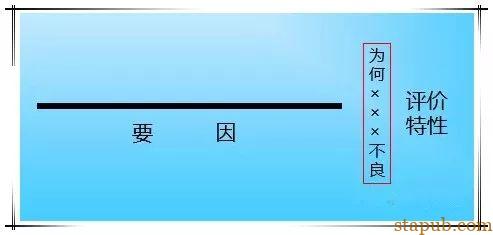
2、大要因以方框圈起来,加上箭头的大分枝到横粗线。
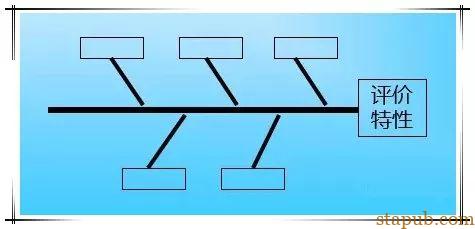
在圈会中全员发言,用集思广益的方法,以收集众人构想的一种思考活动,由于在圈会中刺激每一个人动脑,对问题做创造性思考,促使激荡湃,如暴风雨来袭,故称为脑力激荡法。
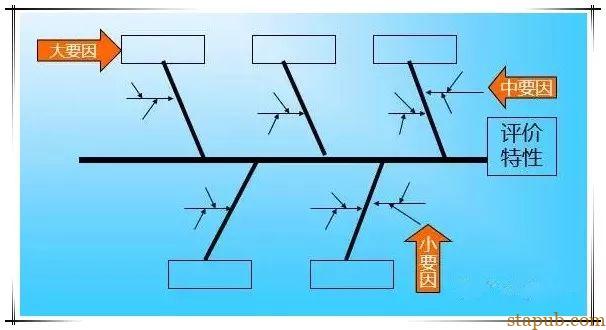
间接部门由圈员以中、小要因之类别予以归纳,再确定大要因。
这些重要要因是作为下一步骤查检的依据,当然圈选时仍需借助于大家的经验以及现场实际的状况来判定。
1、制品名称。
2、作程名程
3、完成日期。
4、参与的圈员及圈长。
1、整理成壁报,张贴现场。
2、必要时,可再召开圈会修正。
在品管圈改善活动,为了便于收集数据与解析判断,而设计的一种表格,查检表。

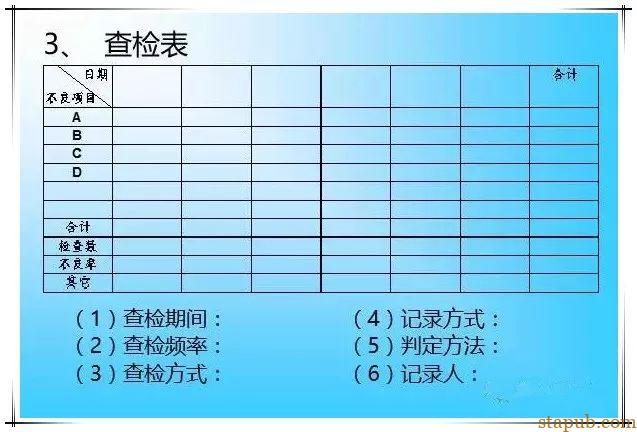
2、迅速记录数字
3、明确履历
4、以符号或数字记录
5、以4~6项为原则
6、必要时修正
将一定期间所收集的不良数、缺点数…….等数据,依项目别、原因别(查检表的项目)加以分类,按其出现大小(大→小)顺序排列的图形。
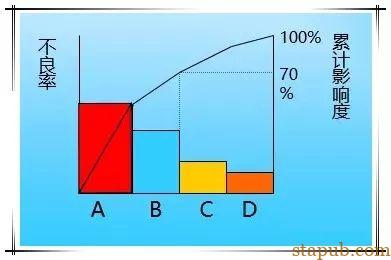
品管大师Juran应用到品管上
品管圈创始人石川馨博士应用到品管圈活动中
(1)以数据为依据分析问题点
(2)掌握全体不良情形
(3)掌握重要不良项目(改善的重点)


(2)横轴距离相同。
(3)纵轴是品质特性,如不良率(数)、缺点数。
(4)最高尺度包含总数。
(5)适用于计数值。
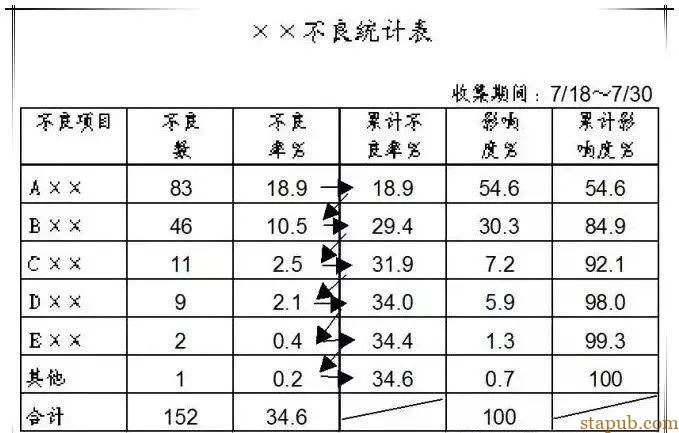
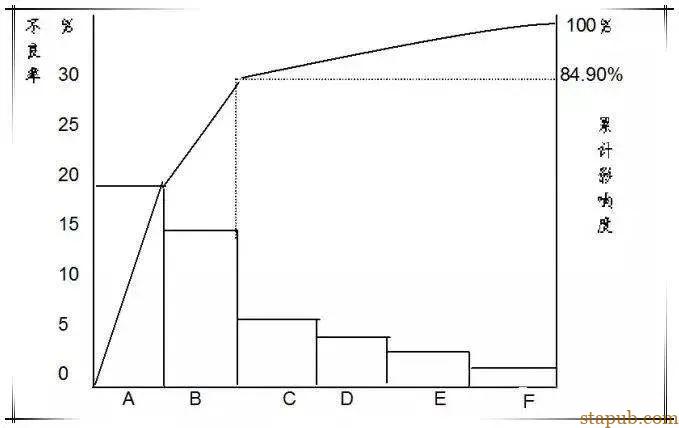
发现原因:从结果到原因,可查出结果如:不良项目别、场所别、工程别,原因如:原料别、机械别、方法别人为别。
报告与记录:只看数据是无法知道分类项目的影响,但柏拉图就能正确的把内容表示出来,可用在报告及记录上。
确认改善效果:把改善前与改善后的柏拉图排列在一起,可以评诂出改善效果。
将某期间所收集的计量值数据(如尺寸、重量、硬度……等)经分组整理成次数分配表,并以柱形予以图式化,以掌握这些数据所代表的情报。

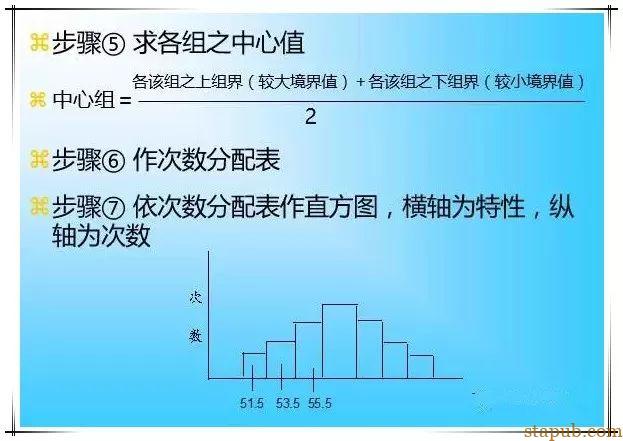
b.离散趋势
c.分配形状
下图是锡膏厚度的直方图,上下限分别是130和220。由图可直接看出数据分布在150~200内, 而170~180间的数据最多。
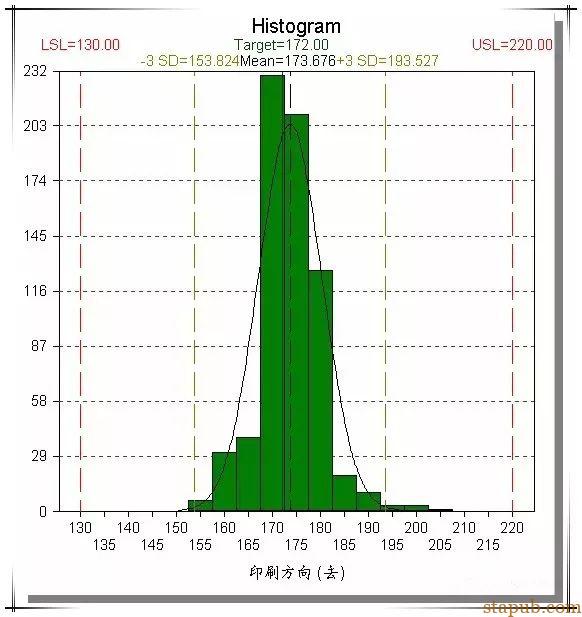
2、分析用--与层别法配合使用,是分析问题的有效工具。
3、调查制程能力。
4、确认效果--可作改善前后比较。
发生品质变异的原因很多,有时很单纯,有时很复杂,但影响其品质的要因不外乎是原料、机器设备、操作人员及操作方法,要找出原因,出自何处,就有分开观察而收集数据的必要。
如果能找出何种原料,那一台机器或那一位操作员有问题后再加以改善,而杜绝不良品的发生。
这种以分层别类的收集数据,以找出期间差异方法,称之为层别法。
1、要迅速有效解决问题,在整个过程中皆需通过比较方式:而要比较一定要层别。
2、以科学思考原则而言观察、假设、证明、结论皆需层别比较。

2、层别分类需符合“周延”“互斥”原则。
3、层别时勿将两个以上角度混杂分类。
4、尽量将层别观念溶进其他手法,如查检表、柏拉图、推移图、直方图、散布图、管制图等。
5、层别后应进行比较(或检定)各作业条件是否有差。
在分析独立数据时,用直方图、柏拉图就可找出改善着眼点,但如要解析两个变量X、Y之间的相关性时,就需使用散布图,将X与Y的两组数据绘在方格纸上,可看出X、Y之间相关情形的图谓之散布图。
如:钢的粹火温度和硬度、镙钉的转距和抗张力、油的温度与粘度、玻璃中含铅量与抗辐射。
先收集两种对应相关的数据,至少要30级以上。
求出数据中X、Y的最大值与最小值。
在横轴( X )与丛轴( Y )上各列出品质要因(特性)。
把两种对应数据点在座标图上。
两组数据相同时另作记号表示。
图上加入品名、工程别、日期、制表人。
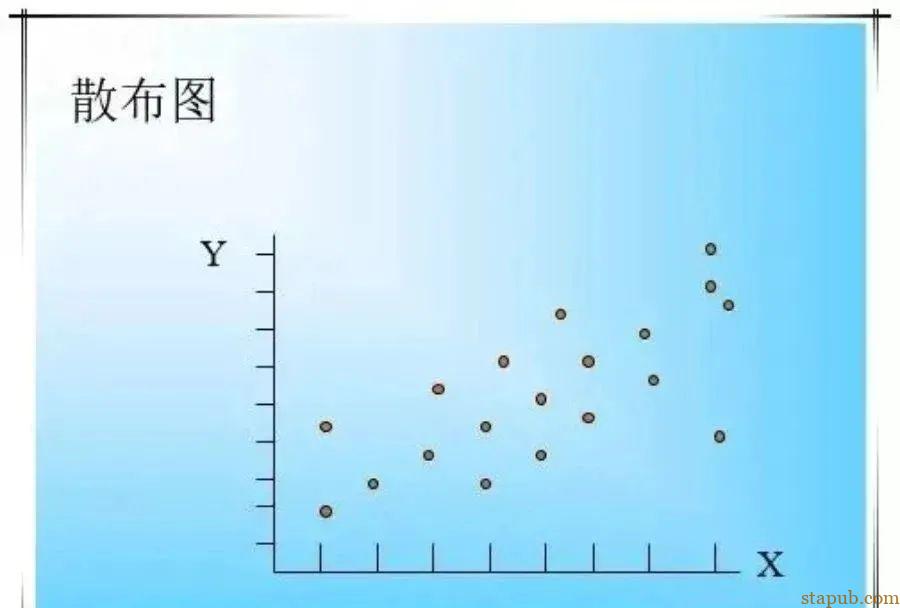
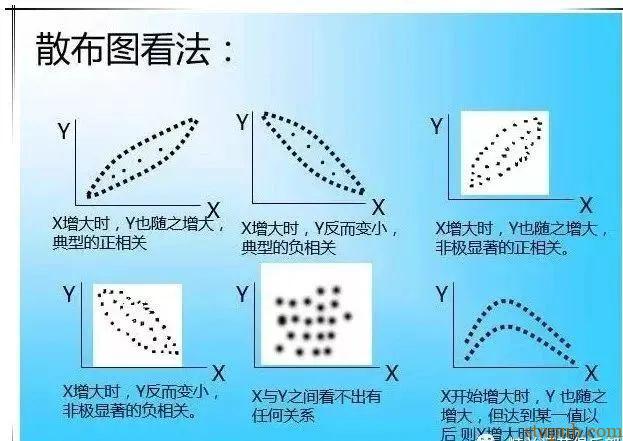
所以,一般管制图纵轴为制品的品质特性,以制程变化的数据为分度:横轴为制品的群体号码,或制造年月日等,以时间顺序、制造顺序将点绘在图上。
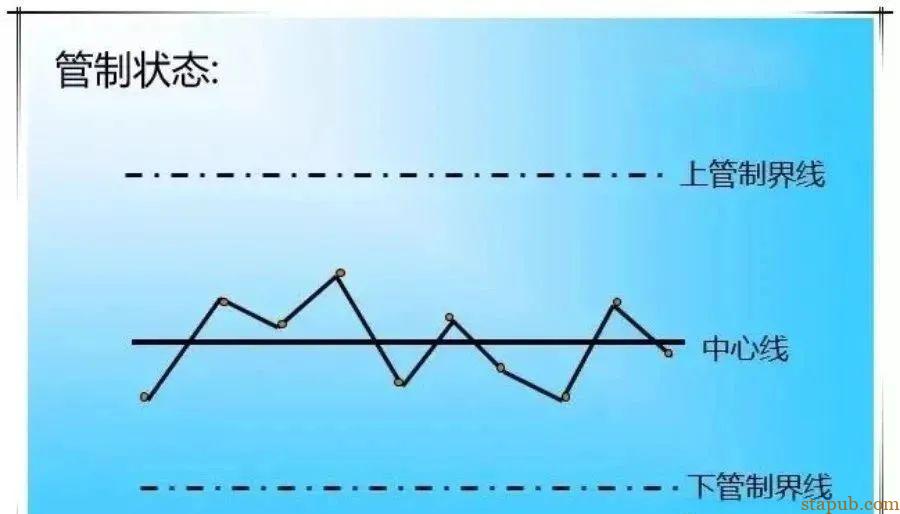
①多数之点子集中在中心线附近。
②少数之点子落在管制界限附近。
③点之分布呈随机状态,无任何规则可循。
④没有点子超出管制界限之外。
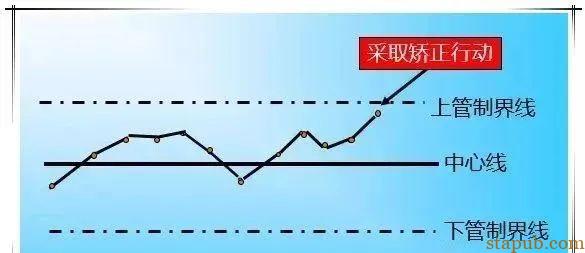
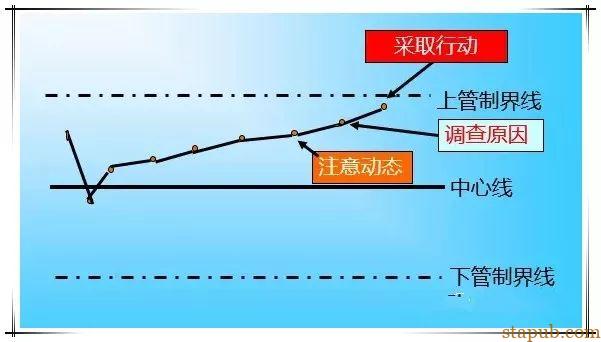
①点在管制界限的线外(或线上)。
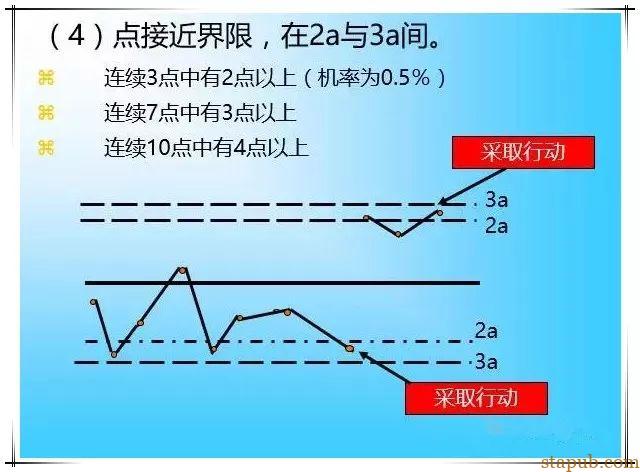
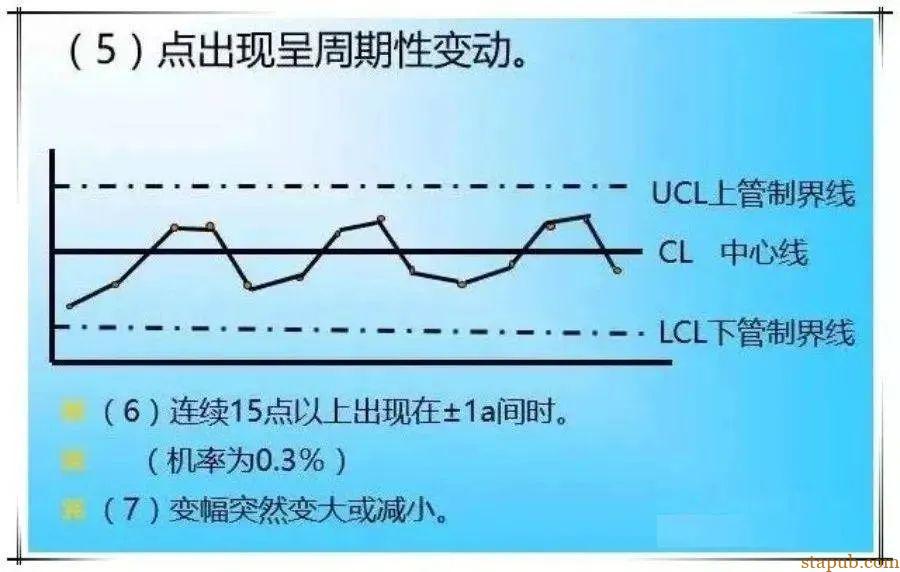
②点虽在管制界限内,但呈特殊排列。
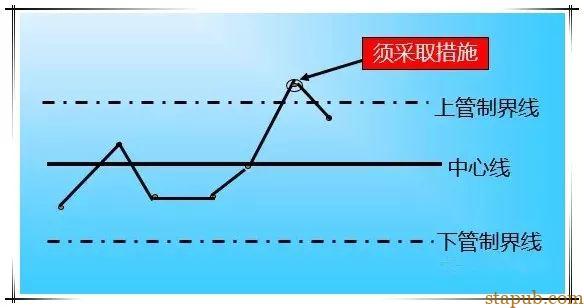
①连续25点以上出现在管制界限线内时(极率为93.46%)
②连续35点中,出现在管制界限外的点不超过1点时。
③连续100点中,出现在管制界限外的点不超过2点时。
制程满足以上条件,虽可认为制程在管制状态,但不是说点超过了界限外也可以,这些超限的点必定有异常原因的,所以必须追究原因,并将之除去方可。
(1)点在中心线单侧连续出现7点以上时,这些点谓之连。(机率为0.8%)
(2)点在中心线单侧出现较多时。
连续11点中至少有10点
连续14点中至少有12点
连续17点中至少有14点
连续20点中至少有16点
后语:大量朋友还没有养成阅读后点赞和分享、转发的习惯,希望大家在阅读后顺便点赞、分享和转发,以示鼓励。积善利他、纯公益性质传播管理知识,长期坚持真的很不容易,坚持需要信仰,专注更显执着,您的支持和鼓励是我坚持的动力!
转自:质量工程师之家











 大师兄
独立事件和卡方检验,都是非常重要的质量管理概念,挺难理解的。
大师兄
独立事件和卡方检验,都是非常重要的质量管理概念,挺难理解的。