MSA手册中分辨力与有效解析度的区别

共计 1320 个字符，预计需要花费 4 分钟才能阅读完成。

在MSA手册中有两个概念，有的学员不理解。一个是分辨力（Discrimination），另一个是有效解析度（Effective resolution）。其实简单地说分辨力是指测量设备可分辨读数的最小单位，也称为最小可读单位、测量解析度。而有效解析度则是指测量系统的分辨力。测量系统的分辨力必须考虑测量系统的重复性和再现性。

问题：一个测量系统中所用的测量设备是最小可读单位为0.02mm的卡尺，用这个测量系统能否分辨10.00mm和10.02mm这两个尺寸？

答案是否定的。这个测量系统中的测量设备（卡尺）的最小可读单位为0.02mm，也就是说卡尺的分辨力为0.02mm。但这个卡尺所构成的测量系统的有效解析度，即这个测量系统的分辨力是否能达到0.02mm还需要考虑该测量系统的重复性和再现性。由于测量系统存在重复性和再现性误差，因此，一般情况下，测量系统的分辨力（也就是有效解析度）都小于测量设备的分辨力，所以尽管测量设备（卡尺）的分辨力可为0.02mm，由该卡尺组成的测量系统是不能分辨出10.00mm和10.02mm这两个尺寸的。

现在让我们了解测量系统的分辨力（也就是有效解析度）是如何确定的。

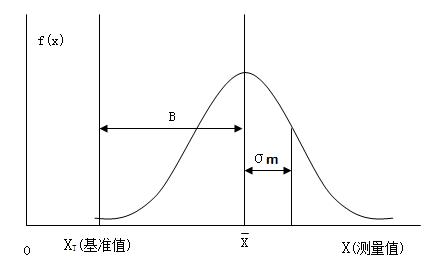
假设已经知道一个测量系统的偏倚为B，重复性和再现性标准差为σm，则采用这个测量系统对一个零件的特性进行多次测量，其测量值X服从均值为X_T+B，方差为σm²的正态分布，其中X_T是零件特性的基准值，见下图：

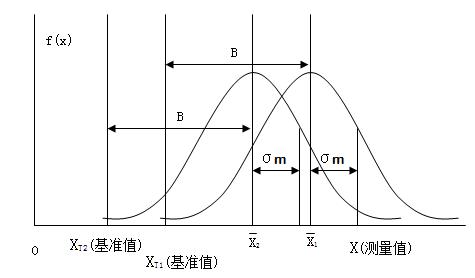
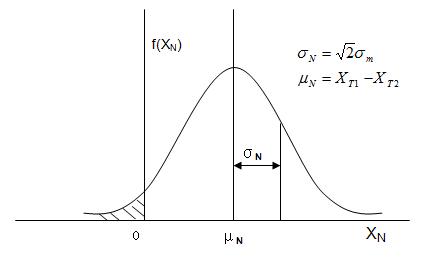
如果用这个测量系统对两个零件的同一特性进行测量，其中一个零件的基准值为X_T1，另一个为X_T2，假定X_{T1 >}X_T2，X_T1的测量值其分布为X_{1 ~} N(X_T1+B, σm²)，X_T2的测量值其分布为X_{2 ~} N(X_T2+B, σm²)，它们的分布如下图所示。可以看出，由于存在重复性和再现性误差，X_T2的测量值X₂可能大于X_T1的测量值X₁，这样就发生了错误分类，即基准值小的其测量值反而大于基准值大的其测量值。

 

为分析发生这种错误分类的概率，现在构建一个新的随机变量X_N，X_N=X₁-X_2。显然X_N也服从正态分布，其均值μ_N= X_T1+B–(X_T2+B)= X_T1– X_T2，方差σ_N²=σm²+σm²=2σm²

当X_N<0时，X₁<X₂，这时就发生了错误分类，所以在X_N<0时的概率P就是错误分类的概率。可以看出，μ_N越大，错误分类概率P越小。

当μ_N=3σ_N时，P=0.135%，错误分类概率很小。

也就是当时，把X_T1和X_T2相互错误分类的概率P=0.135%。

一般把 定义为测量系统的分辨力Δ，即：

测量系统分辨力的意义：当不同零件的被测特性之间的差别 时，测量系统对它们错误分类的概率<=0.135%。

假定一个被测零件特性的基准值服从正态分布，方差为σ_p2，采用一个测量系统对这个特性进行测量。只有当这个测量系统能够可靠地把在零件间的变差（6σ_p）范围内的零件特性值分成5个或更多个数据组时，才能满足为进行统计过程控制而进行测量的要求。这就是测量系统分析中所谓“区别分类数ndc（number of distinct categories）”的概念。

新版（第三版）MSA手册要求区别分类数ndc应圆整（去掉小数位而非四舍五入），且要能大于或等于5。

文章来源：网络