8张图直观讲解SPC八大判异原则(燃爆质量圈)

共计 1399 个字符，预计需要花费 4 分钟才能阅读完成。

当我们要求供应商使用SPC进行过程控制的时候，必然会涉及到的一个问题就是8大判异原则。也就是说，管制图中出现下面的8种点位分布的时候，我们就认为过程出现了特殊原因，我们必须找出点位分布异常的特殊原因，将其消除，从而提前遏制不良品的产生。

作为SQE，你有没有被供应商问及，为啥这8种分布叫做异常分布？今天就从统计学角度，跟大家解释一下，我们通常所说的8大判异原则为啥能够判异，其暗示的潜在异常原因是什么！

首先所有SQE必须要清醒地认识：异常的出现就是小概率事件产生了！

首先给大家解释下正态分布的概率比例，见下图：

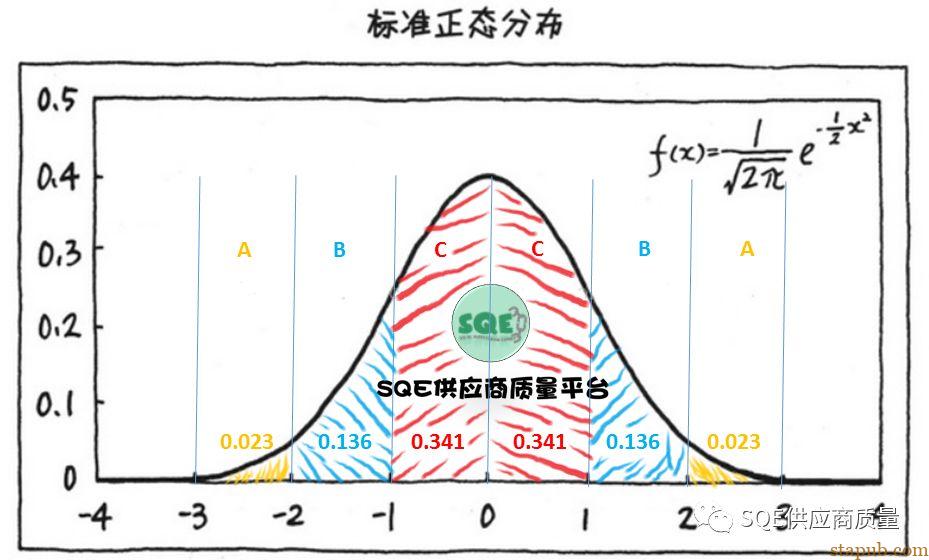
在这张图上，请大家忽略SQE供应商质量平台的logo和名称，专注地记住左A，左B，左C，右C，右B，右A这6个分区；同时在ABC分区的下方都有一个相同颜色的小数：0.023，0.136，0.341(这是样本点出现在相应分区的概率，查表可得，有兴趣，大家可以自己去查表，我们在本文结束的时候有表哦)

好，接下来，我给大家一一解释8大判异入选异常判断准则的缘由：

2/3A（连续3点中有2点在中心线同一侧的B区外<即A区内>）

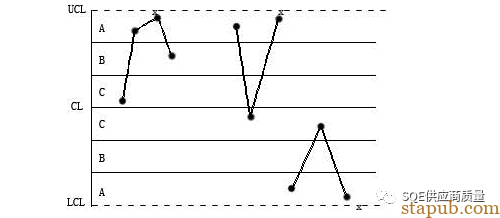
解释： 0.023的平方=0.00529，就是说抽1000数据，才会出现6次这样的情况，小概率事件产生了，肯定有特殊原因导致！

原因：一般认为是新员工，工艺方法错误，机器故障，原材料不合格，测量错误，计算错误，检验方法或标准变化。

4/5C（连续5点中有4点在中心线同一侧的C区以外）

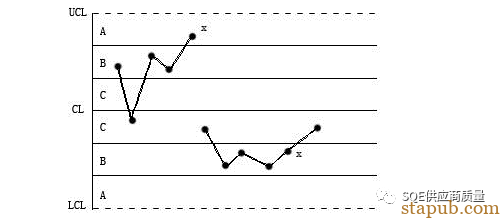
解释：(0.136+0.023)的4次方=0.000639，就是说这种情况出现的概率是千分之六，小概率事件产生了，肯定有特殊原因导致！

原因：一般认为是新员工，工艺方法错误，机器故障，原材料不合格，测量错误，计算错误，检验方法或标准变化。

6连串（连续6点递增或递减，即连成一串）

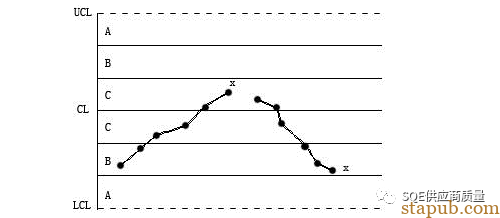
解释：规律分布，必有异因！

原因：刀具模具等工具的磨损，维护保养水平降低，操作工的技能越来越熟练。

8缺C（连续8点在中心线两侧，但没有一点在C区中）

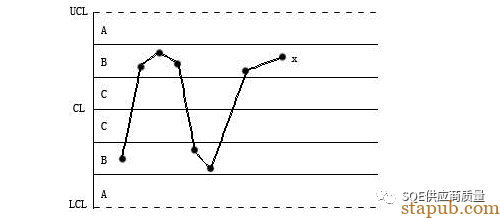
解释：（0.023+0.136+0.136+0.023）的8次方=0.000105，就是说这种情况出现的概率是万分之一，小概率事件产生了，肯定有特殊原因导致！

原因：数据分层不够(SPC没有分模穴去分开做，没有分班次去做等等)

9单侧（连续9点落在中心线同一侧）

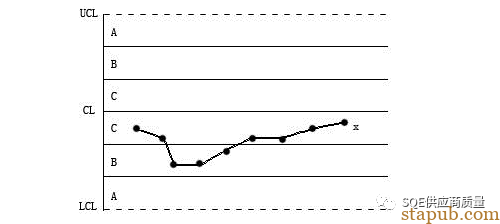
解释：（0.341+0.136+0.023）的9次方=0.00195，就是说这种情况出现的概率是百分之二，小概率事件产生了，肯定有特殊原因导致！

原因：一般认为是新员工，工艺方法错误，机器故障，原材料不合格，测量错误，计算错误，检验方法或标准变化。

14交替（连续14点相邻点上下交替）

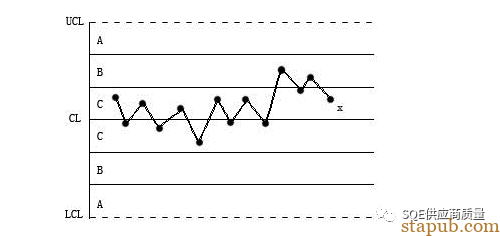
解释：规律分布，必有异因！

原因：轮流使用两台设备或两个操作工操作，分别针对两个模穴定期抽样但一起统计等导致数据分层不够。

15全C（连续15点在C区中心线上下，即全部在C区内）

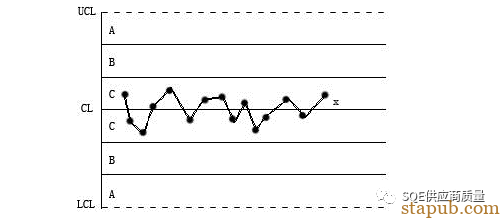
解释：(0.341+0.341)的15次方=0.00321，就是说这种情况出现的概率是千分之三，小概率事件产生了，肯定有特殊原因导致！

原因：数据造假，控制限计算错误太宽了，数据分层不够。

1界外（1点落在A区以外）

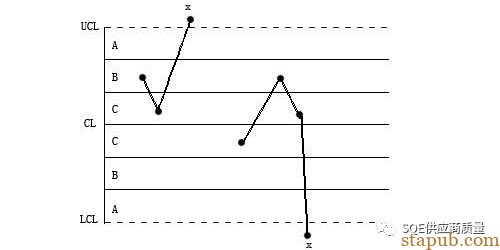
解释：正态分布中出现在ABC分区以外的概率是0，但现在发生了，小概率事件产生了，肯定有特殊原因导致！

原因：一般认为是新员工，工艺方法错误，机器故障，原材料不合格，测量错误，计算错误，检验方法或标准变化。

附：正态分布概率表

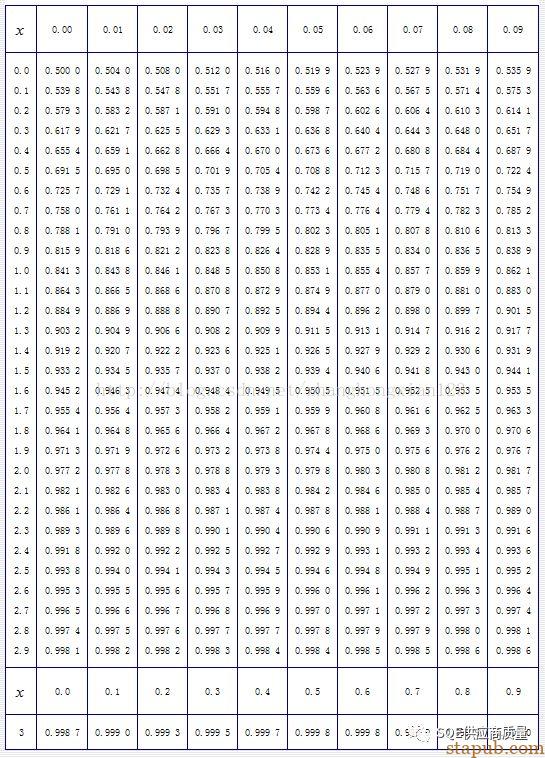
<完>

来源：网络