共计 2344 个字符,预计需要花费 6 分钟才能阅读完成。
“统计学就像比基尼,你所看到的就是真实显露的,但隐藏起来的才是至关重要的”
–无名氏
统计是有一些枯燥,但同时也可以很有趣,不是么?
我们知道统计学包括描述性统计和推论统计,而今天的主题是描述性统计的介绍。
什么是描述性统计呢?维基百科的定义:
“A descriptive statistic is a summary statistic that quantitatively describes orsummarizes features of a collection of information.”
中文翻译:描述性统计是一种汇总统计,用于定量描述或总结信息集合的特征。
这里把关键词勾划一下:
1、Describe-描述
2、Summarize-总结
注意:描述性统计的对象既可以是总体,也可以总体的一部分即是样本。
一、描述性统计的分类
描述性统计又分为
- 集中趋势 Measures of central tendency
- 离散趋势 Measures of Dispersion
1、集中趋势 Measures of Central Tendency
集中趋势又称 “数据的中心位置”,它是一组数据的代表值。集中趋势的概念就是平均数(Average)的概念,它能够对总体的某一特征具有代表性,表明所研究的对象在一定时间、空间条件下的共同性质和一般水平。
常用的集中趋势统计量(statistics)有:
- 算数均值
- 中位数
- 众数
再强调下,在统计学中,这三个统计量都有 average(平均) 的含义。
1、均值 Mean
某组观测值的算术平均数(Arithmetic mean)
2、中位数 Median
按大小顺序排列的数据组之中点位置对应的数值,该数值把数据组分成两半
3、众数 Mode
出现频次最高的观测值。
看起来集中趋势的概念很简单,那么有什么现实价值?
这里我们举两个简化的例子加以说明:
某创业公司A有10个员工,其中1人月薪10万,9人月薪2万;创业公司B也有10个员工,其中1人月薪5万,9人月薪2.5万。
现在假设你要对两家公司员工的收入水平进行对比,你会如何做呢?
通过简单计算我们可得:
公司A:
算术平均 Mean 2.8万;中位数 Median 2万;众数 Mode 2万
公司B:
算术平均 Mean 2.75万;中位数 Median 2.5万;众数 Mode 2.5万
如果看均值 Mean,结果是A公司比B公司高(少数高收入者会把整体平均拉高);如果看中位数 Median,显然B公司更高。
那么应该用Mean还是Median?这取决于我们的目的。
如果我们的目的是研究大多数人的薪资水平,显然用中位数更好,因为B公司90%的人的薪水要高于A公司。
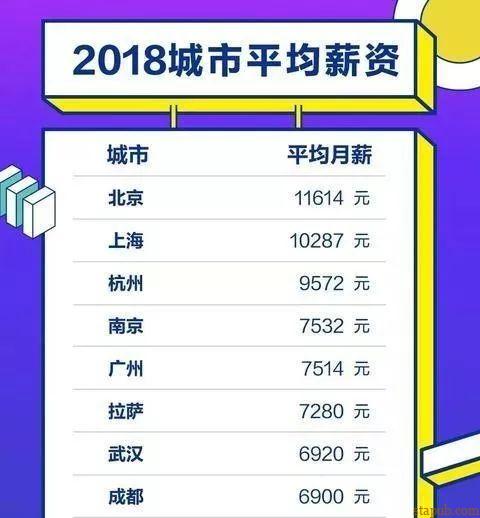
但是在现实生活中,我们往往看到的是用均值mean进行统计说明,尤其是国内媒体,经常用均值来描述某地区某时间段的收入水平。一个不好的结果是,大部分人都会觉得自己“被平均”了。这样做出来的数据固然好看(就像上述公司A),但并不能更准确地展示普通大众真实的收入水平。
看到这里,你应该就能深刻理解“统计学就像比基尼,你所看到的就是真实显露的,但隐藏起来的才是至关重要的”这句话的含义了是不。
二、离散趋势 Measure of Dispersion
所谓离散趋势就是研究观测值偏离中心值(center) 的程度。仅仅研究集中趋势往往是不够的,所以还需要研究离散趋势Measure of Dispersion.
常用离散统计量有:
- 极差
- 标准差(方差)
- 四分位数间距
- 变异系数(相对标准差)
1、极差 Range
为一组数据的最大值和最小值之差。极差的计算较简单,但是它只考虑了数据中的最大值和最小值,而忽略了全部观察值之间的差异。极差在SPC控制图中有大量应用。
2、方差或标准差 Variance or Standard deviation
方差和标准差所反映的是一组数据与其均值为代表的中心的平均离散水平。因为标准差的计算应用到每一个变量值,所以,会受到极端值的影响,当数据中有较明显的极端值(outlier)时不宜使用。必须知道这一点,所有方差/标准差分析的前提是:样本总体服从正态分布,如果不服从,就要有补救措施,比如数据转换。
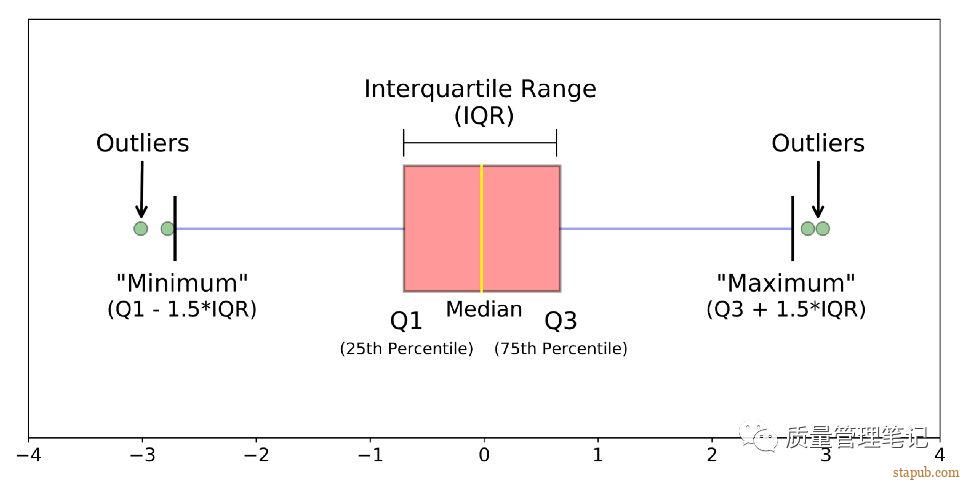
3、四分位数间距 Inter Quartile Range (IQR)
即把所有数值由小到大排列并分成四等份,处于三个分割点位置的数值就是四分位数。第三 “四分位数” 与第一 “四分位数” 的差距又称四分位距, 常和中位数一起使用。比如箱型图。
4、变异系数 Coefficient of Variation (CV)
又叫相对标准差(RSD),变异系数CV是原始数据标准差与原始数据平均数的比。标准差只能度量一组数据对其均值的偏离程度。但若要比较两组数据的离散程度,用两个标准差直接进行比较有时就显得不合适了。例如一个总体的标准差是10,均值是100;如果另有一个总体的标准差是20,均值是2000。如果直接用标准差来进行比较,后一总体的标准差是前一总体标准差的2倍,似乎前一总体的分布集中,而后一总体的分布分散。但前一总体用标准差来衡量的各数据的差异量是其均值的1/10;后一总体用标准差来衡量的各数据差异是其均值的1/100,是微不足道的。可见用标准差与均值的比值大小来衡量不同总体数据的相对分散程度更合理。
三、图形化工具
前文刚开始我们提到关于描述性统计的两个关键词是 Describe(描述) 和 Summarize(总结);同时我们也介绍了可以通过集中趋势统计量以及离散趋势统计量来对目标数据进行描述、总结。但这些统计量基本都是数学计算,比较抽象,有没有更好的方法呢?
答案是有:Visulization!
没错,那就是一系列的图形化工具。
在Excel软件或者Minitab软件都有很多图形化工具用以描述、总结和展示数据,下面摘选部分:
- 柱状图
- 条形图
- 箱型图
- 散点图
- 雷达图
- 气泡图
-End-





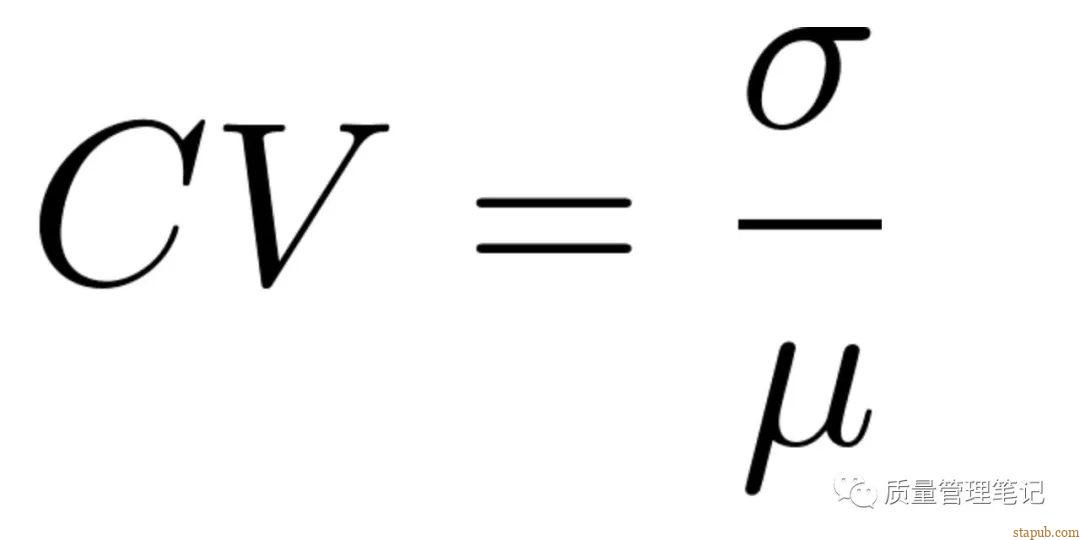










 透彻理解卡方检验 - 汽车质量管理笔记
[…] 化简后的式子是我们在卡方检验中需要用到的式子,所以请大家牢记!对于上述式子有疑惑的读者可以学习基础的概率论,也可以参考我之前写的一篇关于独立的文章(《【直观数学】如何理解两事件间的独立关系》)。如果没有问题的话,我们可以进入到卡方检验原理与步骤的主体介绍部分! […]
透彻理解卡方检验 - 汽车质量管理笔记
[…] 化简后的式子是我们在卡方检验中需要用到的式子,所以请大家牢记!对于上述式子有疑惑的读者可以学习基础的概率论,也可以参考我之前写的一篇关于独立的文章(《【直观数学】如何理解两事件间的独立关系》)。如果没有问题的话,我们可以进入到卡方检验原理与步骤的主体介绍部分! […]