为什么Cpk要大于1.33？原来隐藏了这个成本陷阱

共计 826 个字符，预计需要花费 3 分钟才能阅读完成。

01

CPK与合格率的关系

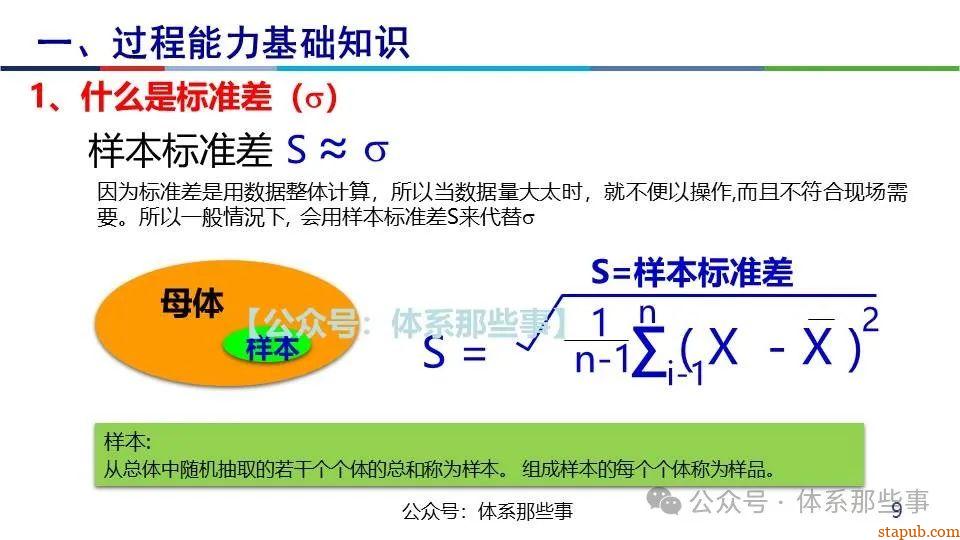
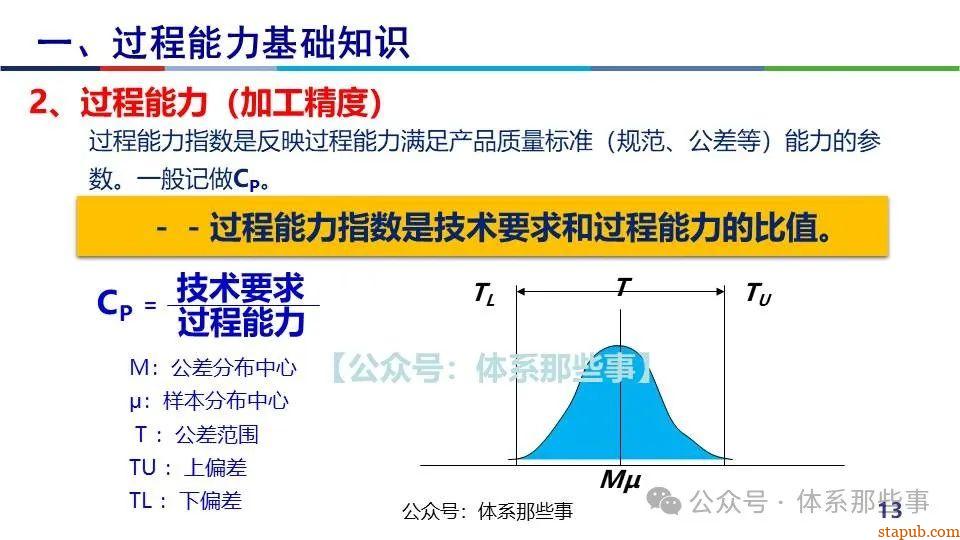
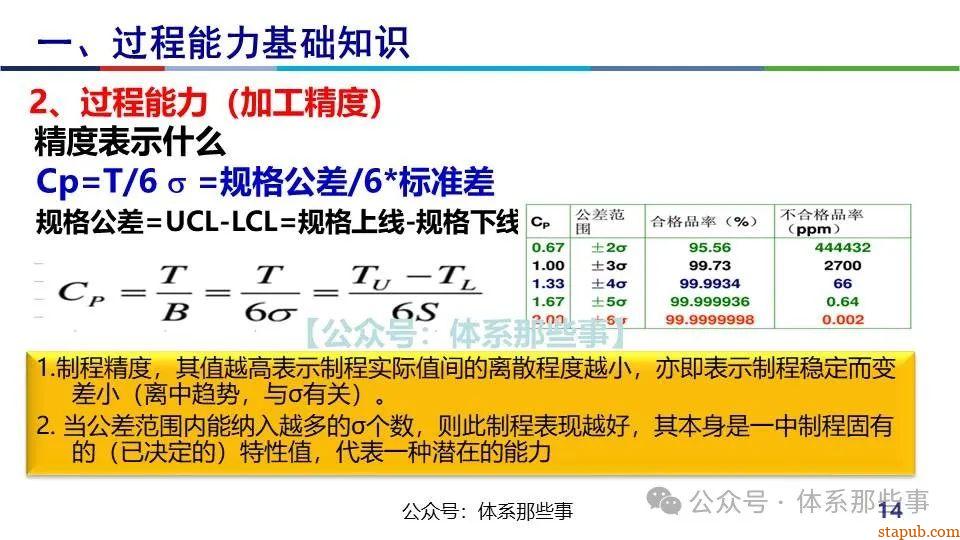
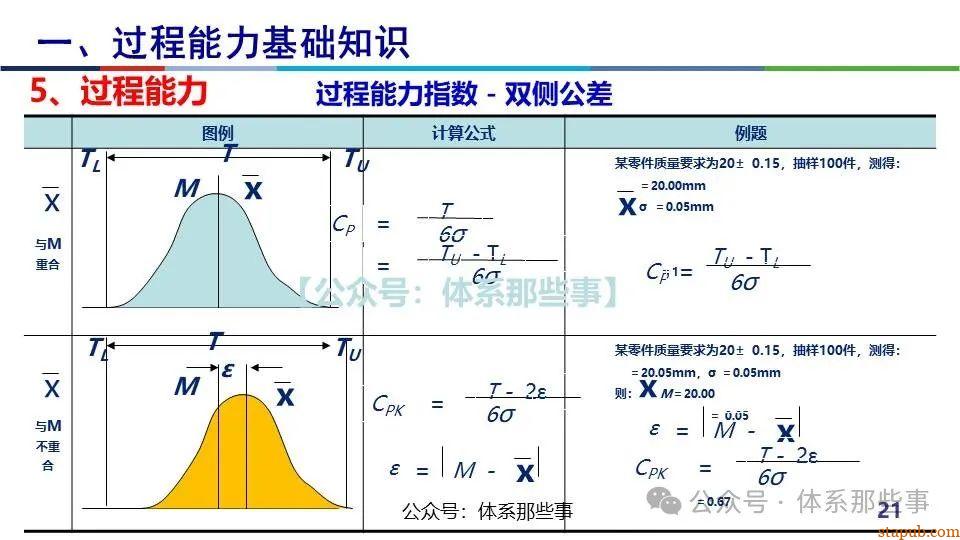
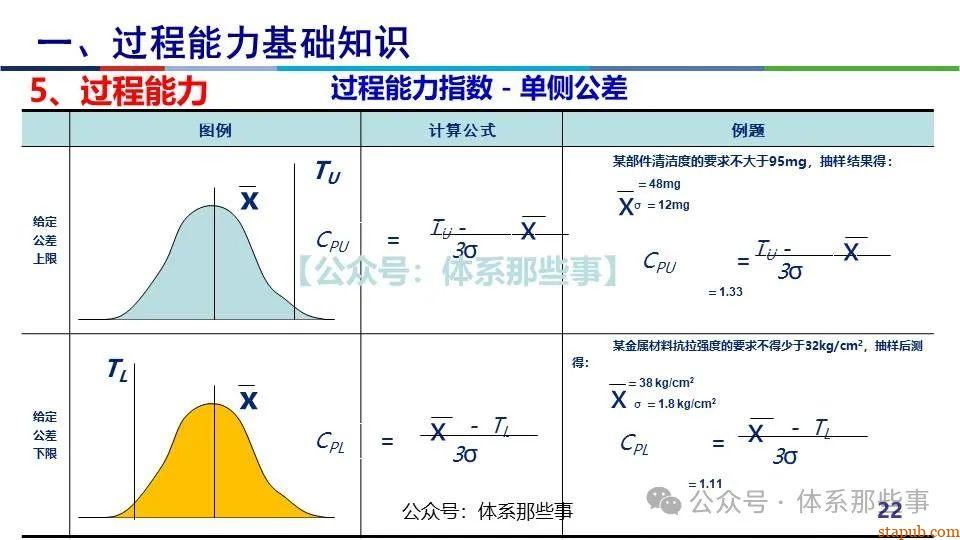
Cpk衡量的是过程输出满足规格要求的能力，计算公式为：

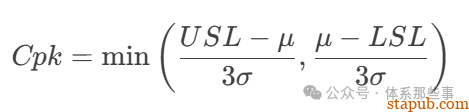
其中：

• USL/LSL：规格上下限
• μ：过程均值
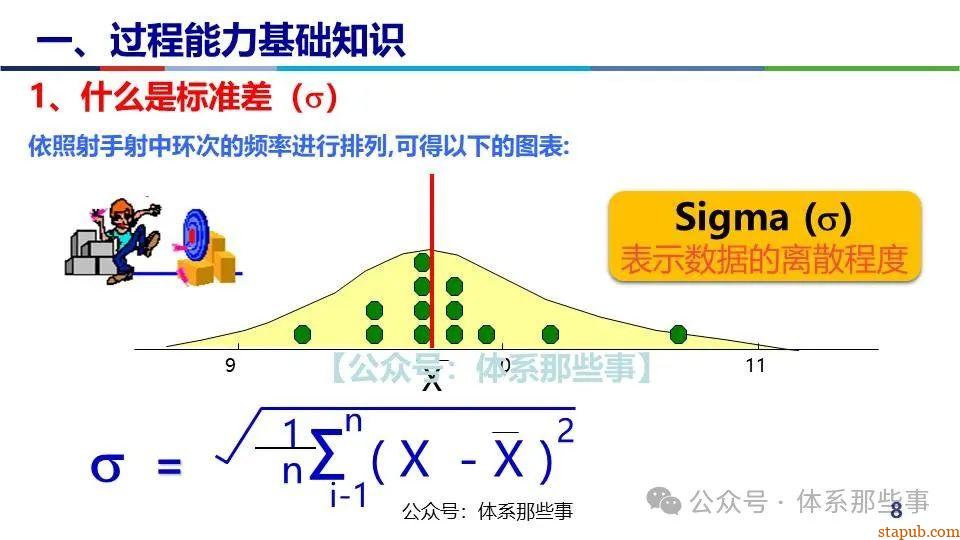
• σ：过程标准差

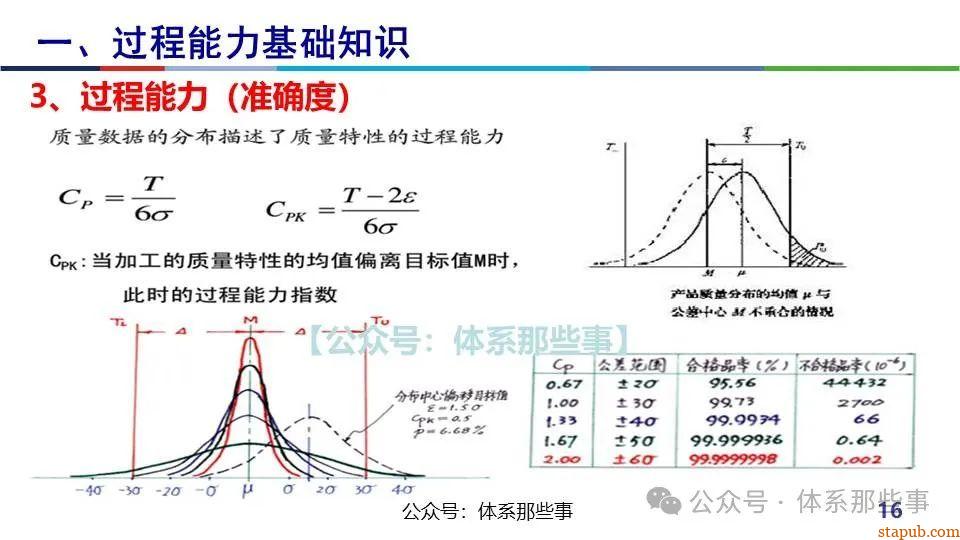
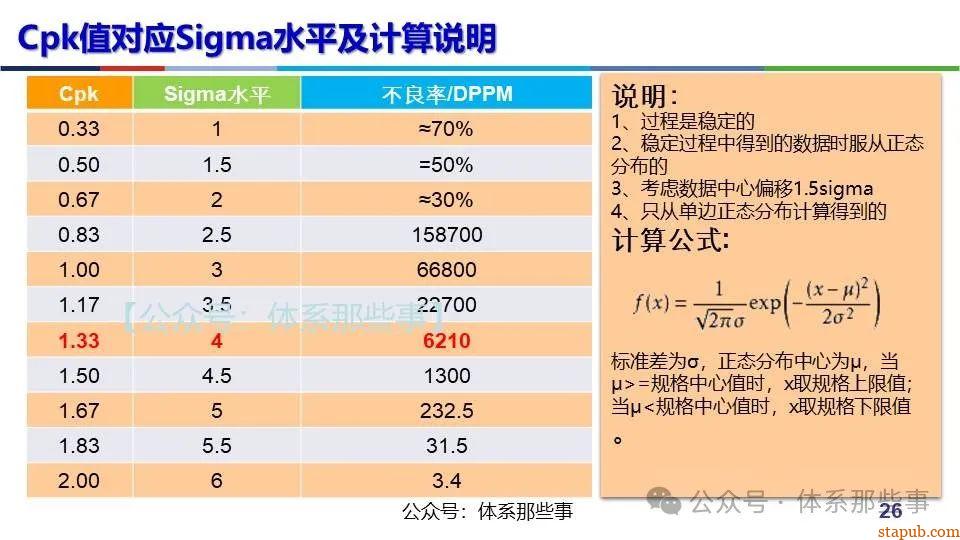
当Cpk=1.33时，意味着过程均值与最近的规格限之间有 4σ 的距离（因为 1.33×3σ≈4σ1.33×3σ≈4σ）。根据正态分布

• 理论合格率：99.994%（仅0.006%的不合格率，即6ppm）。
• 实际缓冲：即使过程均值发生小幅偏移（如±1.5σ），合格率仍能保持在99.38%（6210ppm），满足大多数企业要求。

02

行业中的关键因素

1、预防变异和偏移

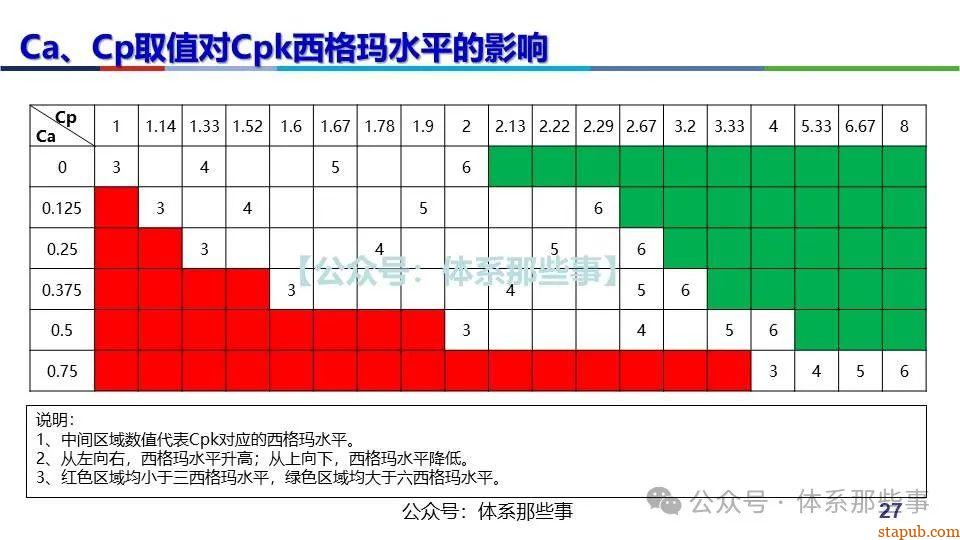
生产过程中难免存在均值偏移（如设备磨损、原料波动等）。Cpk≥1.33为过程提供了安全余量，即使均值偏移1.5σ（常见假设），仍能保证Cpk≥1.0，合格率可控。

6σ管理中，Cpk≥1.67（对应5σ水平）是理想目标，但1.33是许多行业的入门门槛。

2、降低质量成本

早期发现缺陷：高Cpk减少返工、报废和客户投诉的成本。

减少检验频次：过程稳定后可放宽检验，节省资源。

3、客户与行业标准

汽车行业（IATF 16949）、医疗器械（ISO13485）等行业强制要求Cpk≥1.33，否则供应商可能被淘汰。

客户合同条款：许多大客户将Cpk≥1.33写入采购协议。

03

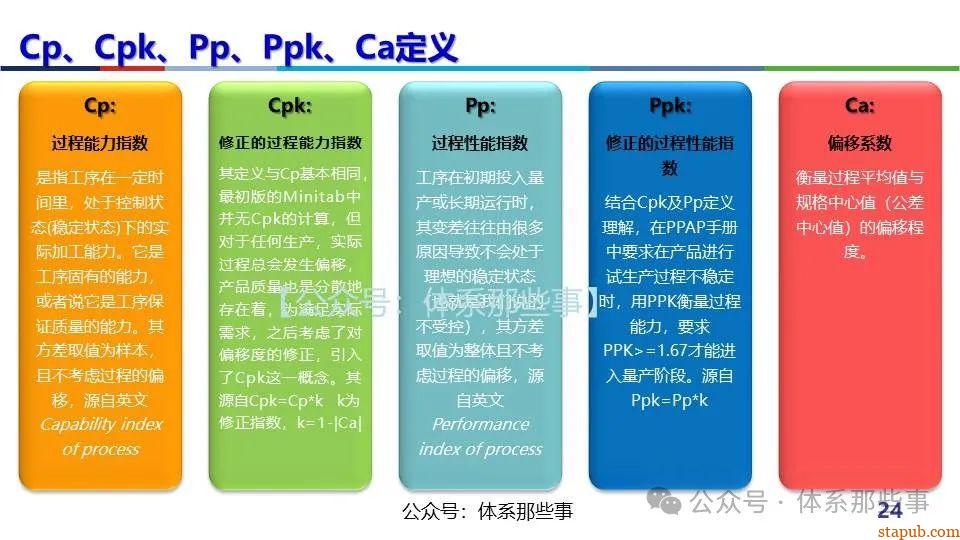
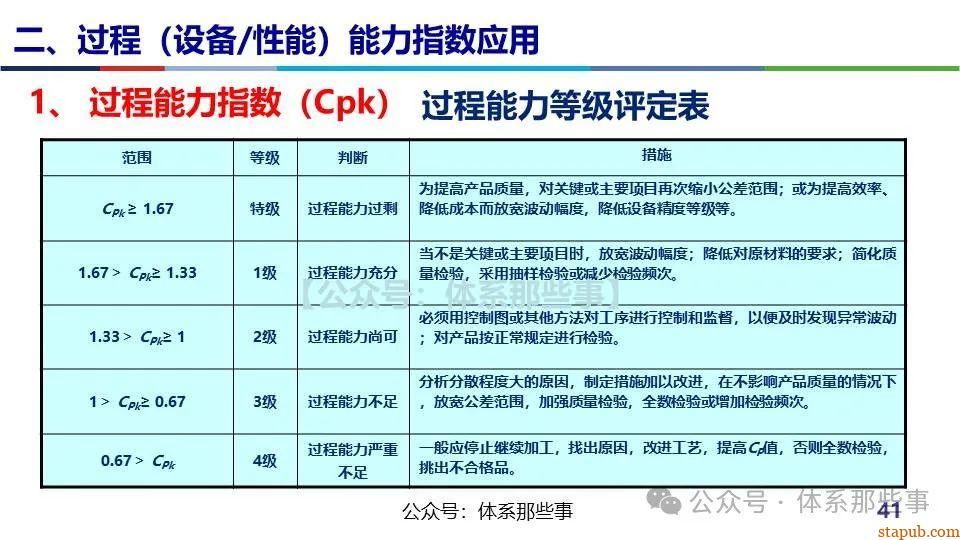
不同CPK值的对比

04

为什么不是更高（如Cpk≥1.67）？

1、成本平衡：

• 提升Cpk需更精密设备、更严格工艺，可能增加成本。

2、必要性：

• 1.33已能满足大多数工业品的质量需求，更高要求仅用于关键领域（如芯片、航空）。

1. 动态监控：
   • Cpk需定期验证，防止过程退化。

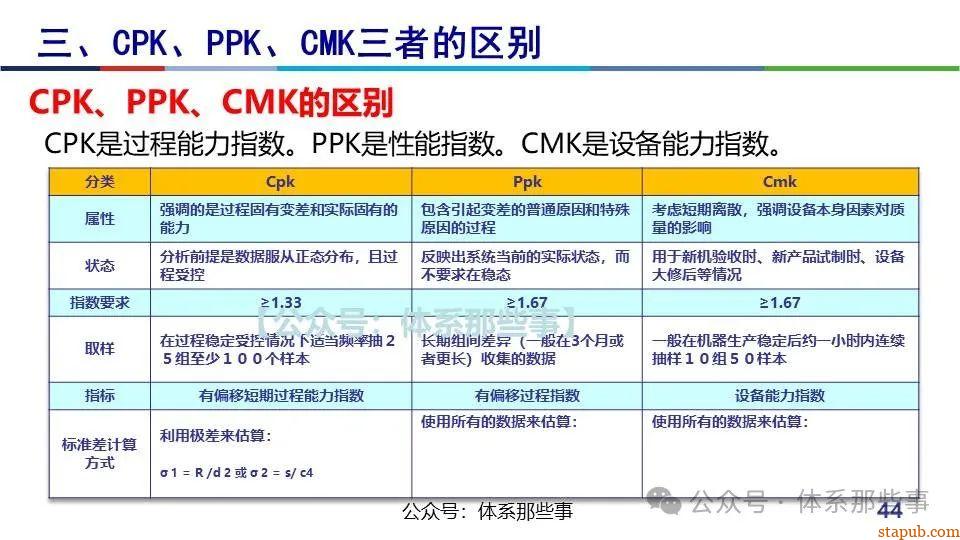
2. 与Ppk区别：

   • 初期小批量生产用Ppk（性能指数），长期稳定后用Cpk。

3. 非正态数据：

   • 若数据非正态分布，需转换或使用其他指标（如Pp/Ppk）。