如何理解两事件间的独立关系

共计 2188 个字符，预计需要花费 6 分钟才能阅读完成。

统计学本质上属于数学的分支，它没有数学那么理论化，但是学好统计学，数学仍旧是必须的。很多从事应用科学的研究者由于既往数理学习的阴影，并不勇于去承认这一点，但这种态度无法改变数学基础学习对统计理解的重要性（有心者稍微去了解一下目前统计领域的顶流-机器学习大多数学生本科背景都可以了，有大量应用数学专业毕业的学生）。

实际上，数学不仅重要，它又是有趣的。很多数学的概念都可以转译为十分直观（intuitive）的常识。麻省理工学院的概率论课本”Introduction to Probability”开篇即引到一则名言：Probability is common sense reduced to calculation. 所以统计的基础-概率论不过是常识的计算版本，繁复的计算背后必可追溯其常识缘起。

遗憾的是，这一直观的常识缘起在日常的数学教学中常常被忽略。数学纯粹沦为某种工具，在教学过程中丧失了其最有趣的部分。“直观数学“这个系列恰恰希望通过对一些小的数理概念进行直观化解释，来尽量弥补一些传统教学中丧失的乐趣，同时在一定程度上帮助读者更好地理解一些偏数理化的统计概念。

独立（Independence）是一个统计领域十分基础的概念，在任何应用统计方法的学科中，我们也经常会看到“独立”这个词。比如在进行抽样时，我们需要保证每一次取样/观察相互间是独立的。那么，这个所谓的“独立”究竟是什么意思呢？

1 “独立”的大白话解释

我们可以先用大白话来理解“独立”：假设有事件A和事件B，两事件独立，指的就是A的发生或不发生，并不影响B事件的发生。举个具体的例子，抛两次硬币，两次的正反面结果是独立的：第一次是正面还是反面，并不会影响第二次的结果，反之亦然。我们还可以看一个“不独立”的例子，比如这一周的天气和下一周的天气，如果这一周整周都是艳阳高照，那么大气会积聚足够的雨量，下周下雨的概率会偏高。这时候我们看到，这一周的天气一定程度上决定了下一周的天气，两事件不独立。

2 “独立”的数学解释

说完了“独立”的大白话概念，我们再来讲一下“独立”的数学表达方式。在这里，我们先要引入一个概念，叫“条件概率”(Conditional Probability)：

如何理解两事件间的独立关系

在上述公式中，等号左边就是典型的“条件概率”表达方式，它可以读作“当B发生时，A发生的概率”。等号右边写明了条件概率的计算方法，也就是A和B都发生的概率，除以B事件的概率。我们可以用经典的Venn图来理解这一计算过程。

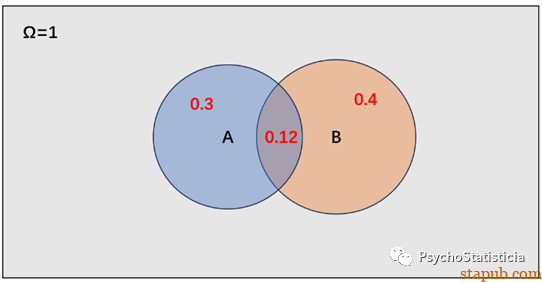
在Venn图中，我们用长方形代表整个样本空间，P(Ω) = 1。现在有事件A, B且P(A)=0.3, P(B)=0.4，则我们可以在这个长方形中绘制一个面积为0.4的圆形代表B事件，一个面积为0.3的圆形代表A事件。当然，这里可以有很多种画法（具体哪一种取决于事件A, B的关系，见后续），但我们姑且假设A, B间有面积为0.12的重叠：

如何理解两事件间的独立关系

这时，如果我们需要计算P(A|B)，也就是在B发生的前提下，A发生的概率，我们就需要聚焦在事件B上，把B看作一整个样本空间（因为规定了前提），然后计算在这个样本空间里A发生的概率。由于在B的世界里，A发生的概率仅对应于重叠部分P(AB)。所以P(A|B)=0.12/0.4=0.3。

在讲完“条件概率”的概念后，我们就可以通过条件概率来理解独立。两事件独立的大白话是指，不管一事件发不发生，都不会影响另一事件的发生。翻译成数学公式，实际上就是：

如何理解两事件间的独立关系

展开条件概率后，这一公式还可被化简为下述公式（化简后的意思并不如原式直观）：

如何理解两事件间的独立关系

3 “独立”的可视化解释

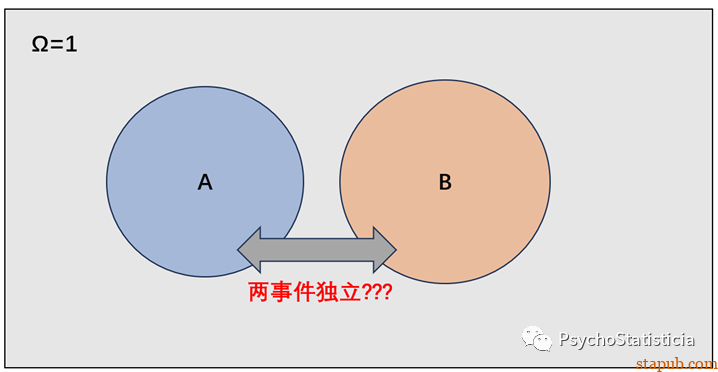
上述讨论了“独立”的大白话解释以及数学公式解释，在数学公式解释过程中我们用到了Venn图。那么，是否可以用Venn图来表示两个独立的事件呢？两个独立的事件是否就意味着下图的表示形式呢？

如何理解两事件间的独立关系

这一惯性思维是极具诱惑性的，很多对独立没有深刻思考的人都会习惯性的认为独立的可视化就是如上图呈现的情况，因为独立好像就意味着两事件没有关系，两事件没有关系就应该没有交集。但上述情况并不代表两事件独立，而代表两事件互斥。至于独立，它恰好对应了我们上述提到的例子，在上述的例子中，我们计算得出P(A)=P(A|B)，这恰恰说明了A与B是独立的，也就是说，A与B独立可以用上述的Venn图来表示：

如何理解两事件间的独立关系

所以，虽然“独立”这个词显得两个事件好像没什么关系，但它并不意味着这两个事件在Venn图上毫无交集。独立在Venn图上的可视化显现可以归结为如下的规律：当事件A和事件B独立时，这恰恰说明在Venn图中，存在一个等比例关系：

如何理解两事件间的独立关系

这一等比关系可以这样理解：不管是在整个样本空间中，还是在B的世界中，A发生的概率都是一样的（B发生，并不影响A发生的概率）。同理，有兴趣的读者可以通过图中的面积情况，看一下在B不发生的世界中，A发生的概率与样本空间中A发生的概率是否相同（答案是肯定的：0.18/0.6=0.3）。

Youtube上有个JB Statistics的博主，做了很多直观理解概率论的视频，有关这个概念的讨论，他也有做视频”What Does Independence Looks Like Venn Diagram”，大家可以自行取阅:

https://www.youtube.com/watch?v=pV3nZAsJxl0

上述就是有关两事件独立关系的讲解，后续我们会从两事件独立的情况推广到多事件的情况。

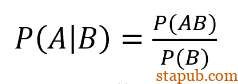
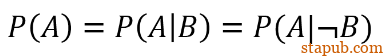
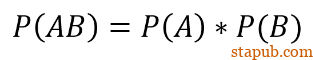
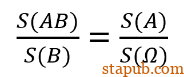
透彻理解卡方检验 - 汽车质量管理笔记 […] 化简后的式子是我们在卡方检验中需要用到的式子，所以请大家牢记！对于上述式子有疑惑的读者可以学习基础的概率论，也可以参考我之前写的一篇关于独立的文章（《【直观数学】如何理解两事件间的独立关系》）。如果没有问题的话，我们可以进入到卡方检验原理与步骤的主体介绍部分！ […]

infinite cui 需求VDA6.3 表格，谢谢

准备与BMW配套？这些要求都知道了吗 – 汽车质量管理笔记 […] 《看看宝马是怎么培训供应商的~》（点击可查看）。 […]

大师兄说的挺有道理的，从现实看到的大部分情况，做技术的人都比较直，对技术的一丝不苟，容易在遇到需要展现管理能力的时候，就会表现出短板来。管理需要授权，更多应该思考团队、部门间，人员发展，对未来的变化做出应对等的能力。

大师兄抱歉，暂无PPT可供下载。

john 如何获得这个PPT文件

大师兄里面确实有一些叫法和我们平时不一样

大师兄这个案例来自一本教科书，短短一页不到的案例描述，有可能漏掉某些细节。我想马自达的员工不会不知道这点，很可能是案例没有提到。马自达的员工更愿意偏离规范不过是这本教科书的猜测罢了。因为象传输系统这么复杂的产品，做得好与做得不好都可能有多个原因。我从另一个案例分析中发现，马自达的最终产品还是比福特的更满足规范要求。变更控制是必要的。

PeriMasto 这个写的不错，很实用，谢谢！

生产、质量及技术三个难兄难弟的关系 | 汽车质量人小馆 […] 附：《生产质量管理十六字精髓》（点击可查具体讲解） […]

透彻理解卡方检验

如何理解两事件间的独立关系

如何判定一个人“工作能力强”？

人如何快速破圈：深度自我分析的力量

注塑模具结构最清晰的讲解

橡胶制品质量提升：橡胶素炼的必要性与作用解析

执行力差只是现象，管理不善才是本质

我为什么反对在属性数据MSA中用Kappa分析(上)

新版FMEA的参数图（P图）有了新格式

整车入库(终检)检验规范