共计 1265 个字符，预计需要花费 4 分钟才能阅读完成。

在机器学习中，我们经常需要从有限的样本中推断出总体的特征。这就需要用到统计学中的一个重要概念—参数估计。

本文将带你了解一下如何通过样本数据来估计总体参数。

什么是参数估计？

参数估计是指在统计学中，根据从总体中抽取的样本数据来推断总体参数的过程。

总体参数是描述整个总体特征的数值，如总体均值（）、总体方差（）、总体比例（）等。

由于总体一般是无限的或足够大的，我们通常无法直接获取总体的全部数据，因此需要通过样本数据来估计这些总体参数。

“通俗来说，参数估计就像是品酒师通过品尝一小杯红酒来推断整桶酒的风味、品质和可能的陈年潜力的过程。

品酒师依赖于他们的感官和经验来做出判断，而统计学家则使用数学和统计方法来做出推断。两者都在有限的样本信息基础上做出关于整体的结论。

一、点估计与区间估计

参数估计主要分为两种类型：

1.点估计(Point Estimation)

点估计是指用单个样本统计量来估计总体参数的过程。它提供了一个具体的数值，作为对总体参数的最佳猜测。

如果我们要估计一个学校学生的身高平均值，我们可能会测量一部分学生，然后用这些样本数据计算平均身高，这个平均值就是一个点估计。

2.区间估计(Interval Estimation)

区间估计提供了一个数值范围，这个范围以一定的置信水平（如95%）包含总体参数。这个范围通常被称为置信区间。

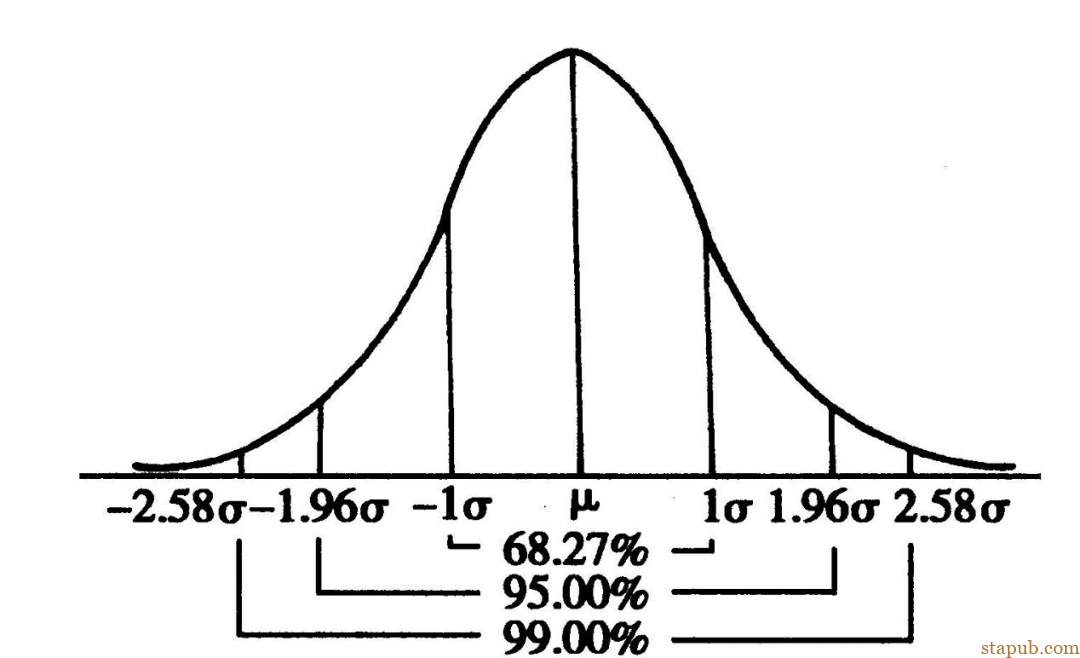
继续上面的例子，如果我们说学生的身高平均值的95%置信区间是160到170厘米，这意味着我们95%确信总体平均身高在这两个值之间。

3.置信区间

在点估计的基础上，在一定的置信水平下，给样本统计量加上一个区间范围作为总体参数的取值范围，这个区间叫置信区间。

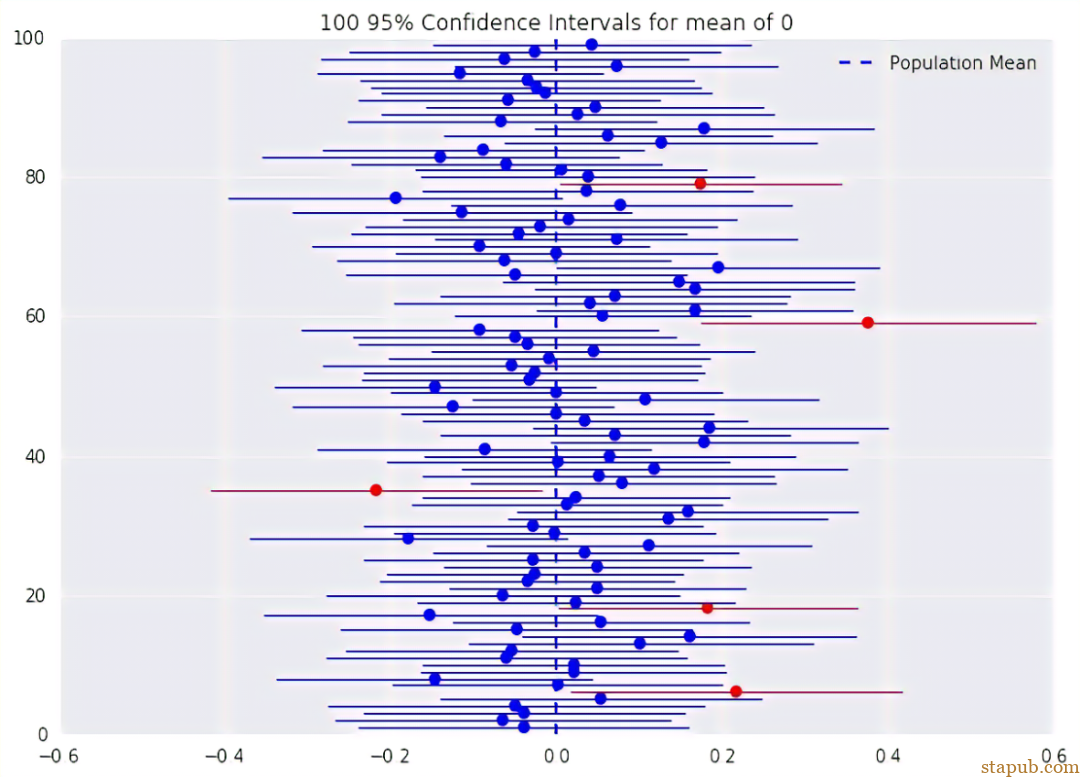
置信区间是区间估计的核心，是统计学中用来表示对参数估计不确定性的一种方法。

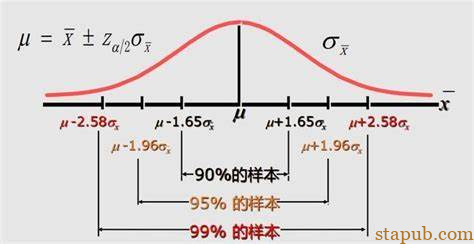
常见的置信水平有95%、99%等，意味着如果多次进行抽样，估计的置信区间将包含总体参数的真实值的比例。

二、参数估计的方法

不同的参数估计方法适用于不同的场景：

• 最大似然估计：一种选择参数值以最大化模型似然函数的方法。似然函数表示在给定参数下，观测到当前样本数据的概率。
• 贝叶斯估计：结合了先验知识和样本数据，通过贝叶斯定理来更新对参数的估计。它将先验分布与似然函数结合，形成后验分布。
• 最小二乘法：一种在回归分析中常用的估计方法，它通过最小化误差的平方和来估计模型参数。

三、参数估计的评价标准

一个好的估计量应该具备以下特性：

• 无偏性：估计量的期望值应等于总体参数的真实值。这是评价估计量是否系统性偏离真实值的重要标准。
• 一致性：随着样本量的增加，估计量应以概率趋近于总体参数的真实值。一致的估计量保证了估计的长期稳定性。
• 有效性：在所有无偏估计量中，具有最小方差的估计量被认为是最有效的。有效性衡量了估计量的精确度。

总结

参数估计在科学研究、工业生产、经济分析等多个领域都有广泛的应用。它帮助我们从有限的数据中获取对总体的深入理解。

尽管参数估计非常有用，但它也有局限性。估计结果可能会受到样本选择偏差、测量误差、模型假设不准确等因素的影响。

参数估计的艺术在于从有限中探索无限。