共计 1808 个字符,预计需要花费 5 分钟才能阅读完成。
球头销在独立悬架系统和转向系统中被广泛采用,主要功能是实现车轮上下跳动和转向运动。控制臂和转向拉杆通过位于端部的球头销与转向节相连接。球头销的安装精度直接影响车轮的运动特性,从而影响车辆的驾驶性能,球头销的安装可靠性影响车辆行驶安全。保证球头销和转向节的连接精度和可靠性是接头设计的重要课题之一。
球头销和转向节的连接采用圆锥过盈连接,过盈量δ是通过拧紧螺母使球销杆伸长实现的,所以计算校核螺母扭矩M和螺母需要转过的转角θ,获得工艺参数,是接头设计必须要做的工作。
今天,螺丝君分三个步骤,通过计算一个实例说明诸多物理量和参数之间的逻辑和数量关系。
– 第一部分
把球头销等效为一根六角头螺栓,计算螺栓的刚度。
– 第二部分
根据过盈连接理论,利用过盈量δ求出螺栓受力。
– 第三部分
说明螺栓轴力与螺母扭矩M和转角θ之间的关系,同时说明螺母的扭矩及转角和球销的进给量的关系。
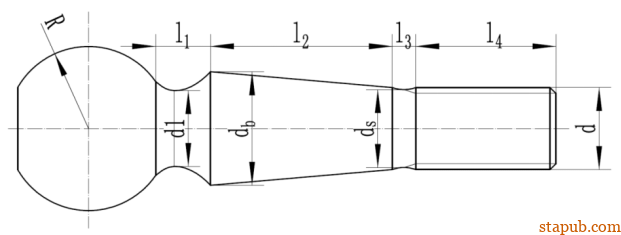
因为在整个扭紧装配过程中,球销杆都参与伸长变形,为了求解刚度时计算简单,保证精度,将球头销等效看作一根螺栓,球头相当于螺栓法兰面头部,球销杆锥体和它的两端过渡部位相当于螺栓的三个光杆部位,尾部是螺纹部分。
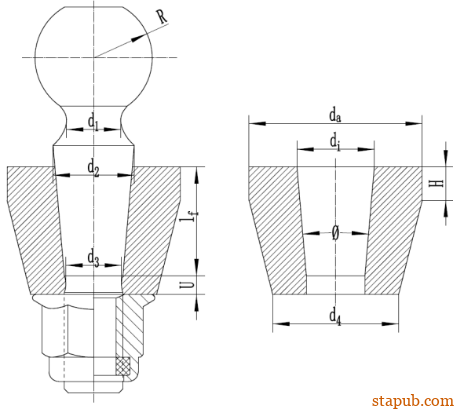
本文中的球头销结构尺寸如下:
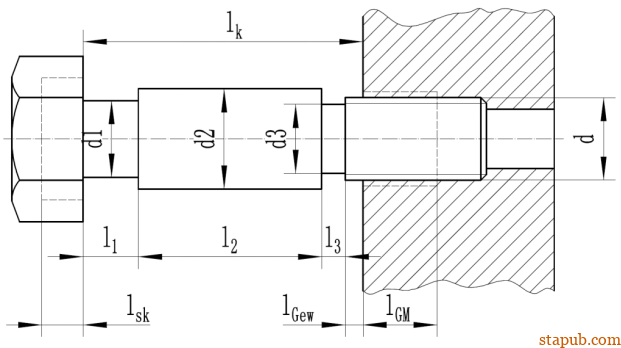
将整个球销等效为如下图的螺栓:
螺栓直径d = 14mm;
螺距P = 1.5mm;
中径

小径

弹性模量ES = 205000N/mm2。
球头和球销杆锥面部位连接的部位直径d1=18.3mm,长度l1=4.756mm。用锥面的平均直径作为中间第二段光杆的直径
长度 l2 =36.125mm。
第三段光杆的直径d3=11.7mm,长度 l3 =4mm。
根据高强度螺栓连接的系统计算指南—VDI2230第一部分中的螺栓的刚度计算模型,螺栓的柔度
其中
根据装配关系计算,没有参与啮合的螺纹杆长度
lGEW = 0.5mm,横截面积以螺栓的小径d3计算,
因为是螺母和螺栓连接,所以
所以可以得到球头销杆的轴向柔度:
于是可以得到球销杆的刚度:
转向节的材料为铸铝,
弹性模量Ea=71450N/mm2;
泊松比υa=0.34,
球头销的材料为42CrMo,
弹性模量Ei= 205000N/mm2,泊松比υi=0.30。
转向节和球头销杆的的圆锥α,锥度是
转向节的外径da=48.06mm;
最大圆锥直径df2=21.6mm,
平均直径
转向节和球销杆结合面的长度 lf =30.5mm。
根据圆锥过盈连接的计算原理,将转向节作为包容件,将球销杆作为被包容件。求得包容件的直径比
被包容件的直径比
求得包容件的过盈量系数
被包容件的过盈量系数
根据受力分析和相关计算—这一部分本文没有论述,转向节锥孔和球头销杆的锥面传递载荷F所需的过盈量δ=0.08mm。
根据所需要的过盈量,可以计算结合面的压强px,
其中
是转向节和球头销杆的圆锥结合面面积。μ=0.17是转向节和球头销杆的摩擦系数。于是
从上面的公式中,可以看出压入力是PN是过盈量δ的线性函数,设
压入力是球销杆在端头螺纹的扭矩M和转角θ作用下伸长获得的轴向力。如果仅使用扭矩法拧紧,扭矩M和轴向力满足下列公式
其中轴向力FM=PN=71KN,螺纹和螺母端面的摩擦系数取相同的值,
是转向节锥孔小径。
计算求得M =150Nm~230Nm,从扭矩M的数值范围可以看出,如果使用扭矩法,因为摩擦系数的范围很大,如果仅设定一个扭矩M值,是不能保证轴向力的稳定性的。比如取
为了保证有效的过盈量,采用扭矩+转角法拧紧,首先施加一个起始扭矩M’=30Nm,得到轴向力
F1=9~14KN。转角需要提供的轴向力
取较大值FMmax=62KN。
为了获得这个轴向力,螺栓的轴向伸长量
螺栓的径向收缩量
球销杆和转向节直径的变化量总和是过盈量与球销杆收缩量之和
因为直径变化导致的球头进给量
测量螺栓端的位移量
为了获得这一个位移量,螺母的转角
L.S.ENGINEER Experience and Summary
今天,螺丝君在转向节和球头销的装配过盈量和装配工艺参数之间建立了计算关系公式, 以已知过盈量为前提,计算扭矩M 和转角θ,同时计算球头销的进给量和螺栓端的位移量,为装配质量校核提供了检测参数。
![]()
![]()
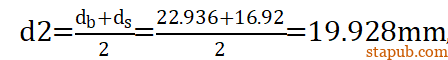
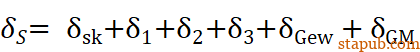
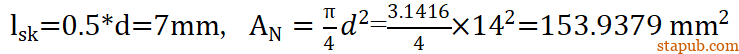
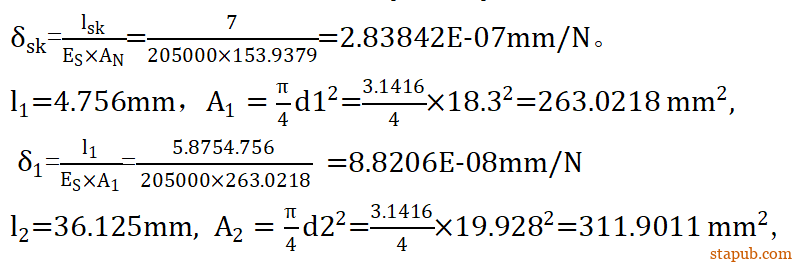
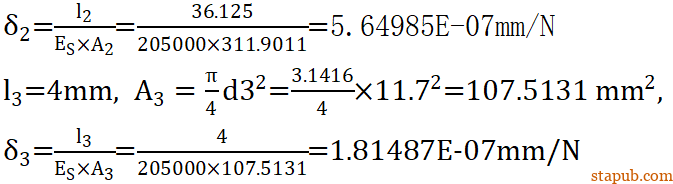
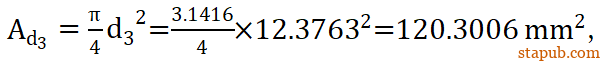
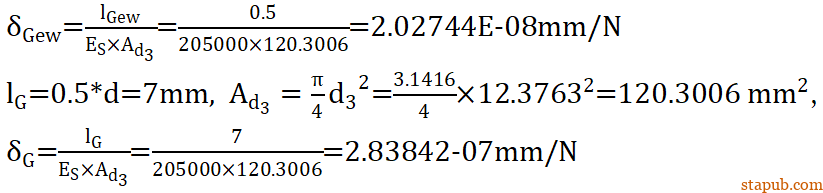
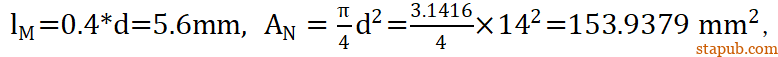

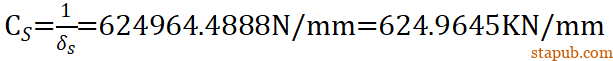
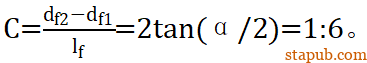
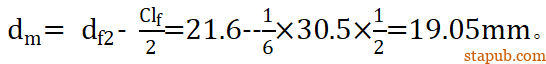
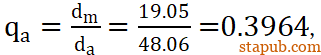
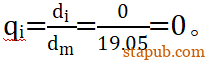
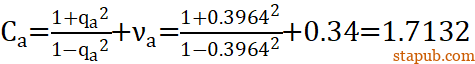
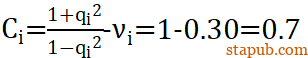
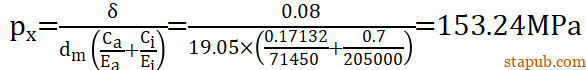
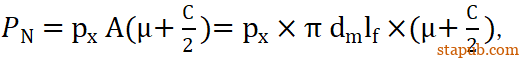
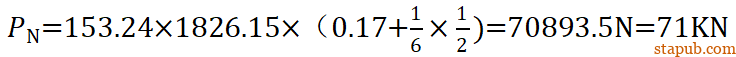
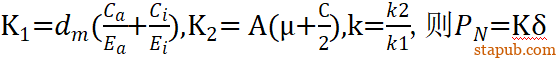
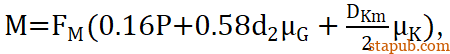
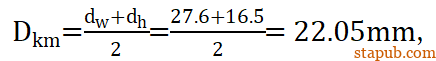
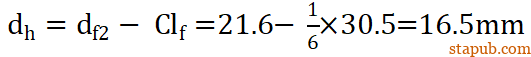
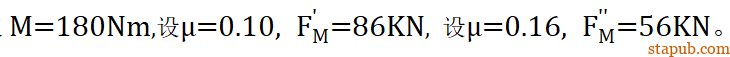
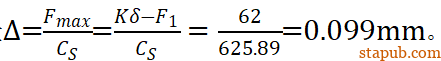
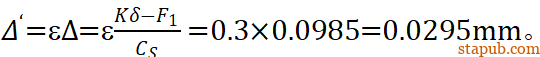
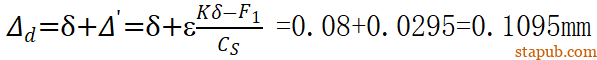
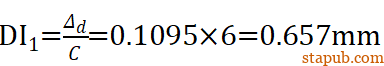
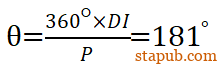










 大师兄
独立事件和卡方检验,都是非常重要的质量管理概念,挺难理解的。
大师兄
独立事件和卡方检验,都是非常重要的质量管理概念,挺难理解的。




