我为什么反对在属性数据MSA中用Kappa分析(上)

共计 1839 个字符，预计需要花费 5 分钟才能阅读完成。

这可能是一篇会引起很多争议的文章，在写完初稿后搁置了大半年的时间，现在略作修改分两次发完，希望能够引起大家的讨论。

熟悉我的人都知道，在MSA中，我明确反对两个东西。

一个是ndc，因为这只是%P/Tv的另一个解释，但却派生出独立的判断标准，使得两个指标之间产生了矛盾，使人无所适从。在《六西格玛管理统计指南》第3版(以下简称指南三)p.405-407有详细阐述，在此不再赘述。

另一个就是属性数据MSA中的Kappa。

一致率、误判率、漏判率这些简单明了的指标足以让我们对测量系统做出恰当的判断，为什么还要画蛇添足地加上一个Kappa呢？很多年来我从来不讲Kappa，在蓝皮书里也只是简单提了一下，并没有做详细的阐述。但这也没有什么用，Kappa分析仍大行其道，又像ndc一样，成为了一种教条。

虽然明确反对使用Kappa分析，但说实话，我自己也信心不足，毕竟对此没有多深入的了解。为此我做了一些功课，也有了一些心得。在此提出来与各位探讨，欢迎拍砖。

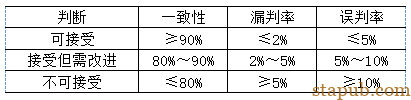
我们先看看针对属性数据的一致性标准。

这样的标准表述比较清晰，很容易理解，也比较容易得出结论。

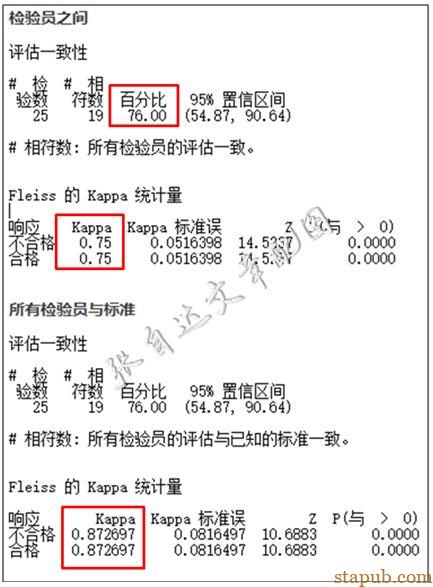
再看看Kappa的标准，大于0.9可接受，介于0.7~0.9可勉强接受，小于0.7不合格。但0.7或0.9的实际意义是什么，与一致性有什么关系，却没有说清楚。在实际应用中，当Kappa的结论与一致性的结论矛盾时，往往让人无所适从。如下面这个案例：

从分析结果上中，评估一致性以及与标准的一致性均只有76%，但Kappa值却有0.75和0.87。根据上述标准判断，一个是不合格，一个是可以让步接受，那应该怎么下结论呢？如果判定不合格，但Kappa却显示可以用，尤其是后一个，都接近0.9了；如果判定可接受，但明明一致性不好啊。

类似的不协调也出现在%P/Tv和ndc之间，这里不再赘述。

为什么会出现这种结果呢？本文试图从Kappa分析的原理来做一探究。

Kappa分析有两种。

一种是Cohen’s Kappa，只能用于分析对同一组对象两次评价的一致性，如一个人先后两次评价的一致性、一次评价与标准的一致性、两个人对同一组对象评价的一致性等。具体原理参见拙作《列联表篇之二：四格表的分析》。

另一种就是大家熟悉的Fleiss’ Kappa，可以用于对同一组对象的多次评价的一致性分析，目前流行的属性数据MSA就是采用这种分析。具体原理参见拙作《列联表篇之十：属性相同双向有序表的Kappa分析》。

首先用Cohen’s Kappa做一个热身。

在四川大学王军2006年的硕士论文《Kappa系数在一致性评价中的应用研究》中，总结了三种反例。其中之一如下例:

这个案例中，一致率达到了0.704，但算出的Kappa值却只有0.006，这明显不符合常理。更进一步看下一个例子：

这两个案例的一致率都是0.8，但Kappa值却相差很多。

问题出在四格表中左上角a和右下角d取值不平衡上。可以想见，a和d相差越大，Kappa值越小。

我们可以做一个模拟，来看看Kappa值是如果随a、d的取值变化的。

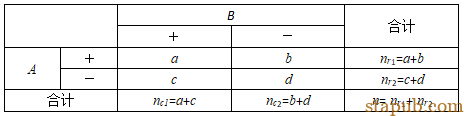
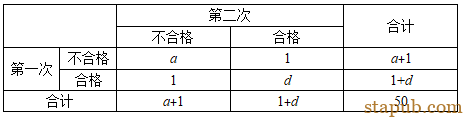
为了方便使用Cohen’sKappa，假设在属性一致性分析时，选择了50个样品，由一个人重复测量2次。构建的四格表如下：

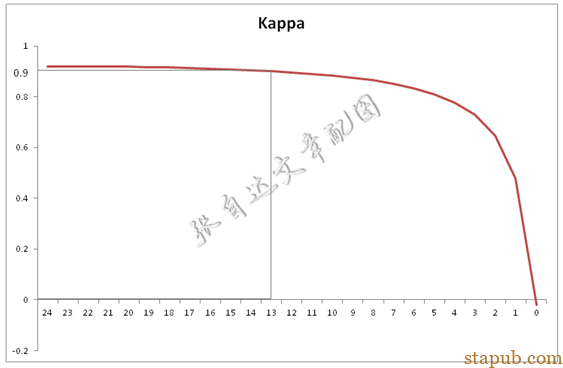
为了分析方便，我们固定取b和c为1，这样可以计算出一致率P0为0.96，这应该是很高的一致率了。a取值从24逐渐减到0，同时d从24逐渐加到48，我们可以看看Kappa值呈现怎样的变化。

可以看出，当a减少到13时，Kappa值降低到0.9以下，当a继续减少时，Kappa值会快速下降，这时就会出现判据不一致的问题。

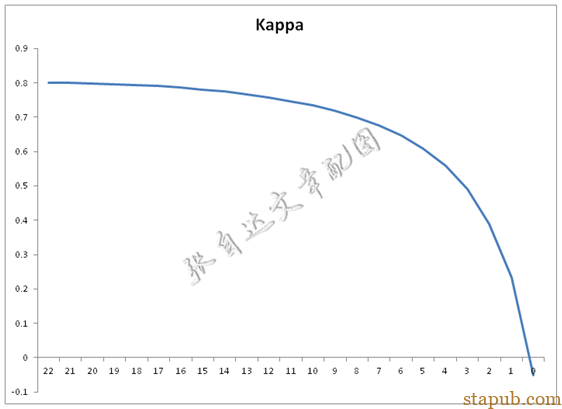
如果将一致率降低到0.9，则Kappa的变化曲线是这样的。

此时Kappa最大只有0.8，也就是说，即使一致率达到了90%，因为Kappa均在0.8以下，因此也不能得出测量系统合格的结论，又产生了判断不一致的情况。

由上面的初步分析可以看出，Kappa值的大小依赖于样本的结构。如果MSA样本中合格与不合格品数量差异很大，则会得到小的Kappa值。如果你想得到比较Kappa值与一致率大致相当的结论，建议尽可能保持合格/不合格样本量的平衡。

在不了解样本结构时直接根据Kappa下结论是危险的。即使Kappa值为1，如果样本全部是非常容易判断的产品组成的，那么这个结论也是值得怀疑的。反过来说，即使Kappa值不高，但样本构成中包含大量难判断的产品，结论也不是不可接受，需要进一步分析检验员判断错误的实际情况后作出恰当的结论。

来源：张老师漫谈六西格玛