共计 2719 个字符,预计需要花费 7 分钟才能阅读完成。
BMS的主要任务是检测电池工作情况、估算电池SOC、电池健康状况(State of Health,简称SOH),完成热管理、充放电控制、CAN(Controller AreaNetwork)通信、均衡检测、故障诊断和液晶显示等功能,使电动汽车的控制单元能够及时有效地利用所传递的SOC等信息,对动力电池的过充或过放有防止作用。电池组的均衡技术,快速充电技术和电池SOC估算是电池管理系统的三项关键性技术。
电池荷电状态(State of Charge,简称SOC),指电池中剩余电荷的可用状态。SOC定义有多种多样。目前在国际上比较统一的是从容量的角度给予定义,即荷电状态SOC表示电池的剩余容量,其在数值上等于电池剩余容量与额定容量的比值。
电池荷电状态SOC作为描述电池状态的一个重要参数,对其进行准确地估算是当今电池研究的一个难题和热点。因此,如果能够对SOC进行准确的估算,那么将会对电池的研究和发展起着举足轻重的作用。目前己经出现了很多较为精确的SOC估算方法,下面列举几种主要的方法:
1、放电测试法
放电测试法将动力电池以一定的放电倍率(一般为0.3C或1C)进行恒流放电至电池的截止电压,将恒值电流(C 0.3 C或1C)乘以放电所用的时间可以得到电池放出的电量,即电池SOC值。
该方法常被用来作为电池容量测试的参考标准,适用于各种类型的动力电池。但是,这种方法的测试条件比较严格,需要电流恒定且测量准确,以至于只能局限于实验室环境下所测得的数据。在实际应用中,电流大小并非恒定,且电流经常会被迫中断,也需要消耗过多的时间,不可能有实验室中稳定、可靠的理想环境,因此,该方法不适合实际应用。
2、开路电压法
开路电压法是根据电池的开路电压(OpenCircuit Voltage, OCV)与电池内部锂离子浓度之间的变化关系,间接地拟合出它与电池SOC之间的一一对应关系。在进行实际操作时,需要将电池充满电量后以固定的放电倍率(一般取1C)进行放电,直到电池的截止电压时停止放电,根据该放电过程获得OCV与SOC之间的关系曲线。当电池处于实际工作状态时便能根据电池两端的电压值,通过查找OCV-SOC关系表得到当前的电池SOC。
尽管该方法对各种蓄电池都有效,但也存在自身缺陷:首先,测量OCV前必须将目标电池静置 1h 以上,从而使电池内部电解质均匀分布以便获得稳定的端电压;其次,电池处于不同温度或不同寿命时期时,尽管开路电压一样,但实际上的SOC可能差别较大,长期使用该方法其测量结果并不能保证完全准确。因此,开路电压法与放电试验法一样,并不适用于运行中的电池SOC估算。
3、电流积分法
电流积分法也叫安时计量法,是目前在电池管理系统领域中应用较为普遍的SOC估算方法之一,其本质是在电池进行充电或放电时,通过累积充进或放出的电量来估算电池的SOC,同时根据放电率和电池温度对估算出的SOC进行一定的补偿 。如果将电池在充放电初始状态时的SOC值定义为SOCt0,那么t时刻后的电池剩余容量SOC则为:
与其它SOC估算方法相比,电流积分法相对简单可靠,并且可以动态地估算电池的SOC值,因此被广泛使用。但该方法也存在两方面的局限性:其一,电流积分法需要提前获得电池的初始 SOC值,并且要对流入或流出电池的电流进行精确采集,才能使估算误差尽可能小;其二,该方法只是以电池的外部特征作为SOC估算依据,在一定程度上忽视了电池自放电率、老化程度和充放电倍率对电池SOC的影响,长期使用也会导致测量误差不断累积扩大,因此需要引入相关修正系数对累积误差进行纠正。
4、人工神经网络法
神经网络法是模拟人脑及其神经元用以处理非线性系统的新型算法,无需深入研究电池的内部结构,只需提前从目标电池中提取出大量符合其工作特性的输入与输出样本,并将其输入到使用该方法所建立系统中,就能获得运行中的SOC值。
人工神经网络算法用于电池SOC估算时,常采用电池的开路电压、充放电倍率、环境温度和电池表面温度等其中几个参数组合或全部作为输入变量。有研究者将电池容量的衰减度作为输入变量,应用于不同尺寸的电池和不同容量衰减程度的电池时,运算结果都表现出一定的精确性。该方法用于电池SOC估算有着很多的优点,但同时也存在计算量大,耗时,需要大存储空间,需要训练样本等一些问题。
5、模糊逻辑法
模糊逻辑方法是基于模糊逻辑推理理论,模仿人的思维方式系统的方法,对难以建立精确数学模型的对象实施的一种控制策略给出的一种描述控制。
不同于经典逻辑,需要一个精确的数学模型和准确的数值,模糊逻辑则允许使用来源于我们的知识和生活经验的抽象概念来建模,用诸如大、小、非常热、明亮的红色、长时间、快或慢等主观概念来表述。与数值系统相比,这种算法的开发相对简单,然后将系统输出映射到精确的数值范围来表征系统特性。模糊控制广泛应用于自动化控制系统中,使用该算法,可以获取大量能表征电池性能的信息,以对电池SOC或者SOH更准确的估计,能够对电池状态进行一个较为全面的分析监测。
6、系统滤波法
相对于前述的几种方法,系统滤波算法具有闭环控制和实时性强的优点,因此目前被广泛应用于电池SOC估算,最常用到的系统滤波算法是卡尔曼滤波算法。
卡尔曼滤波是在20世纪60年代由美籍匈牙利数学家卡尔曼(R.E.Kalman)提出来的,他将状态空间分析方法融合到滤波理论中,自其问世以来,卡尔曼滤波作为一种最优状态估算方法,可以应用于受随机干扰影响的动态系统。
准确地说,卡尔曼滤波本质是一种递推算法,可以实时获得的受噪声干扰的离散观测数据,对系统状态进行线性、无偏及最小误差方差的最优估计。因此,卡尔曼滤波算法不仅仅适用于动态的随机过程,而且可以实现递推,通过预测新的状态和它的不确定性,然后采用新的测量值修正校准预测值,非常适用于多输入系统。因此,对于计算机运算,卡尔曼滤波的运算量和存储量较传统方法大为减少,能够满足实时性的要求,目前在工程实践中迅速得到了广泛的应用。
然而,卡尔曼滤波算法作为一种线性算法在应用到非线性系统中时存在一定的困难,因此许多基于卡尔曼滤波算法的的改进算法被提出。
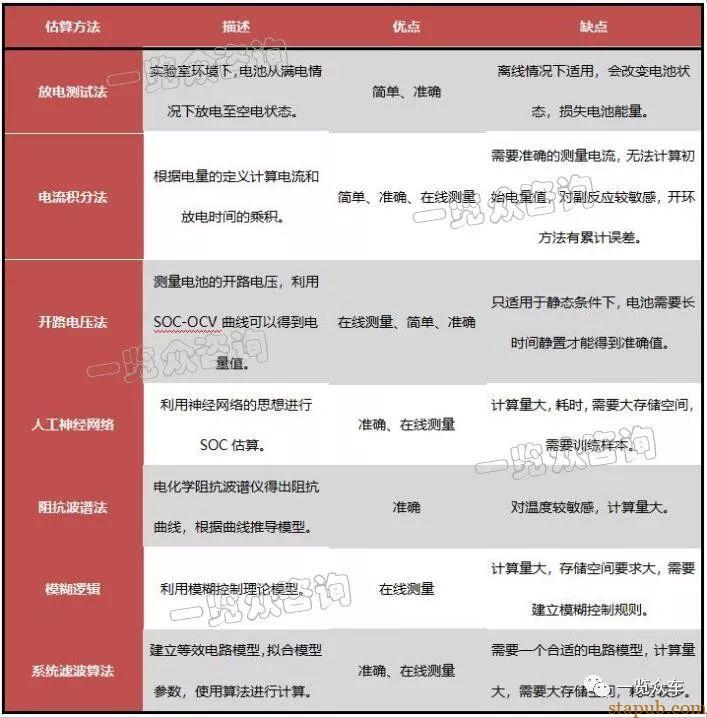
图表 主要SOC估算方法比较
锂离子动力电池的SOC是一个非直接测量变量,不能通过传感器件直接测量得到,只能通过可测量变量结合控制算法进行估算,加之锂离子动力电池的工作过程是一个较为复杂的电化学反应过程,内部状态多变且难以预知,同时在工作时也会受到外部环境多方面因素的影响。
但是在实际应用中,SOC又是一个非常重要的参考量,它是使用者判断电池系统状态的依据。相比较而言,卡尔曼滤波算法及其改进算法是一类较有前途且应用广泛的算法。
来源:一览众车

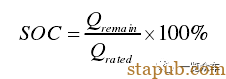
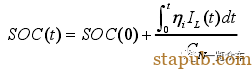








 透彻理解卡方检验 - 汽车质量管理笔记
[…] 化简后的式子是我们在卡方检验中需要用到的式子,所以请大家牢记!对于上述式子有疑惑的读者可以学习基础的概率论,也可以参考我之前写的一篇关于独立的文章(《【直观数学】如何理解两事件间的独立关系》)。如果没有问题的话,我们可以进入到卡方检验原理与步骤的主体介绍部分! […]
透彻理解卡方检验 - 汽车质量管理笔记
[…] 化简后的式子是我们在卡方检验中需要用到的式子,所以请大家牢记!对于上述式子有疑惑的读者可以学习基础的概率论,也可以参考我之前写的一篇关于独立的文章(《【直观数学】如何理解两事件间的独立关系》)。如果没有问题的话,我们可以进入到卡方检验原理与步骤的主体介绍部分! […]