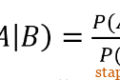共计 3730 个字符，预计需要花费 10 分钟才能阅读完成。
在文章《什么是阶次？》一文中已经讲解了什么是阶次、为什么要关心阶次、怎么计算阶次等内容。但是，我觉得关于阶次的一些方面还没有讲清楚，如阶次的物理意义、阶次与频率的关系、为什么阶次分析中的高阶次不清晰等内容。本文主要内容包括：1. 阶次的物理意义；
2. 阶次与频率的关系；
3. 为什么高阶次不清晰；
4. 阶次实例：扇叶的通过阶次。
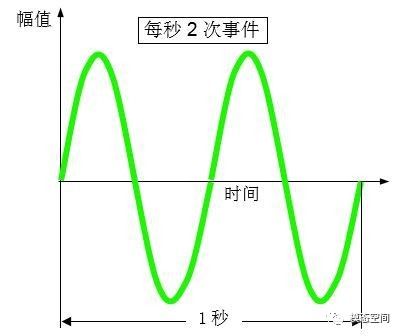
按照振动理论来分，可以把振动分成线振动和角振动。线振动是我们通常所说的常规的振动，用位移、速度和加速度来描述，对应的载荷是力；角振动是旋转振动或扭转振动，用角位移、角速度和角加速度来描述，对应的载荷是力矩或扭矩。一个刚体有6个自由度，分别为3个平动自由度和3个转动自由度，那么平动对应的是线振动，转动对应的是角振动。对于常规的振动（线振动）而言，通常用频率来描述一秒钟内振动往复的次数，这就是所谓的振动频率。如图1所示，在一秒钟内有两个周期，因此，振动频率是2Hz，或者说一秒钟内振动这个事件发生的次数是2次。用时间和频率来描述常规的线振动。
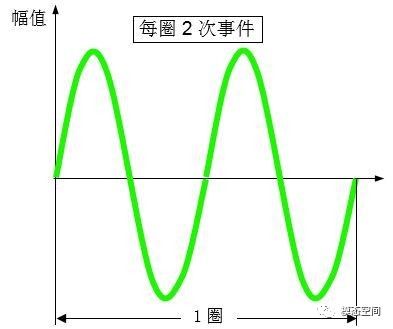
对于扭转振动而言，通常用阶次这个名词来描述，阶次表示的是旋转部件每旋转一圈（360度）事件发生的次数。与阶次相对应的是角度或者旋转的圈数，而每旋转一圈对应360度，因此，圈数与角度是等价的。扭转振动中的阶次与圈数（或角度）对应于常规振动中的振动与时间。如图2所示，横纵表示圈数或角度，那么在一圈内振动的周期是2个，那么振动这个事件发生2次，我们可以说阶次是2阶次。因此，阶次的物理意义是表示每圈事件发生的次数。
对于有质量偏心的旋转部件而言，它的阶次是1阶次，这是因为每旋转一圈，这个质量偏心的事件只发生一次。如果旋转部件的圆形截面变成了椭圆，那么，它的阶次将是2阶次，这是因为椭圆有一个长轴，但长轴有两端，每旋转一圈长轴的两端导致质量偏心出现两次，因此，是2阶次。倘若在旋转轴上有齿轮盘，齿数是29个，那么，齿轮啮合时，每旋转一圈，齿轮碰撞将发生29次，因此，齿轮的阶次是29阶次。对于4缸4冲程发动机来说，首先考虑一个缸，完成一个工作循环需要旋转2圈，才点火一次，因此，单缸每旋转一圈点火0.5次，对应0.5阶次，由于有4个缸，因此，曲轴每旋转一圈点火2次，因而，我们讲发动机的点火阶次是2阶次。所以，阶次是每圈（或360度）事件发生的次数。明白这个物理意义，可以帮助我们深入理解阶次这个概念。
旋转振动用角度和阶次来描述，除此之外，还有一个关键的参数，即转速（是角速度）。转速表示每分钟旋转的圈数，单位为rpm（Revolution Per Minute），如果用每秒钟旋转的圈数来表示，则称为转动频率，简称为转频，是频率的一种表现形式。也就是说转频与转速的关系如下
阶次是表示每圈事件发生的次数，而转频是表示每秒钟旋转的圈数，那么，阶次对应的事件的频率则是阶次乘以转频。因此，1阶次对应的事件的频率是1倍的转频，K阶次对应的事件的频率是K倍的转频，或者说1阶次对应的频率是1倍转频，K阶次对应的频率是K倍转频。不管转速如何变化，这种关系都是固定不变的，因此，我们说阶次独立于转速。阶次对应的事件的频率等于阶次乘以转频，事件的频率不随参考轴的变化而变化的。但是当考虑用不同的旋转轴来表示时，对应的阶次数与轴的转速（或转频）是变化的，但二者的乘积是保持不变的，即事件的频率是不随参考轴变化的。
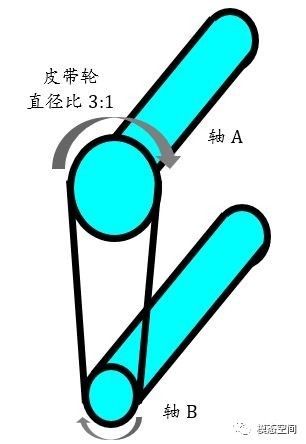
还是使用之前的例子，A轴的直径是B轴的3倍。A轴转速从600rpm增加到6000rpm，同时通过皮带带动B轴旋转。因此，B轴的转速是1800rpm到18000rpm。也就是说B轴的转速是A轴的3倍，B轴的阶次是A轴的3倍，或者A轴的阶次是B轴的1/3。
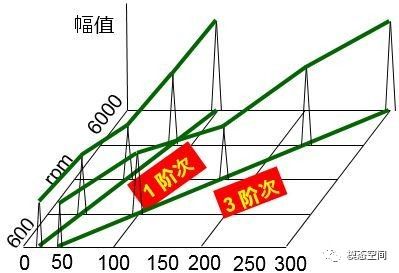
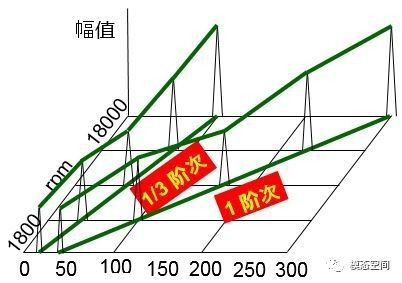
如果考虑A轴的事件的频率等于A轴的阶次乘以它的转频，如果以A轴的转速作为参考，那么A轴对应的事件的频率等于A轴的阶次乘以A轴的转频（1*rpmA/60）。如果以B轴的转速作为参考，此时，A轴的阶次是B轴的1/3，此时A轴对应的事件的频率等于A轴的阶次乘以B轴的转频（1/3*rpmB/60）。因为B轴的转频是A轴的3倍，所以A轴的阶次对应的事件的频率是不变，不管以哪个轴的转速作为参考。同理，B轴的阶次对应的事件的频率也是相同的道理，不以转速参考轴的变化而变化，都是固定不变的。这个例子也说明，同一根轴，当以不同的旋转轴作为参考轴时，其对应的阶次数是不同的，但彼此之间的阶次关系是确定的，由两轴之间的转速转递关系决定。如果当以A轴的转速作为参考时，A轴的阶次是1阶次，B轴的阶次是3阶次。但如果以B轴作为转速参考，那么，B轴的阶次是1阶次，A轴的阶次是1/3阶次。但是A轴与B轴的阶次关系为1：3是不随转速参考轴的变化而变化的。因此，在计算阶次时，将实际测量的转速设置成第1阶次，其他旋转部件的阶次通过结构之间的转速传递关系（传动比）确定其阶次数。
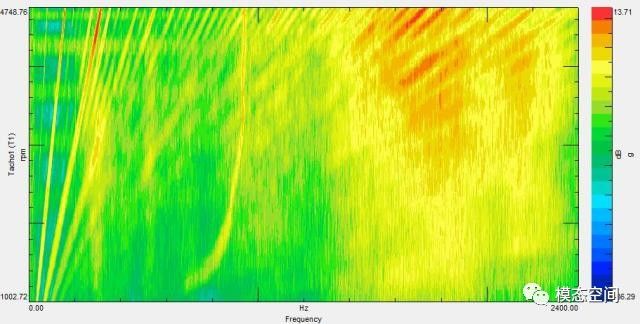
在做阶次分析时，经常发现colormap图中的高阶次成分模糊不清，不利于从这些高阶次中提取有用的信息。如图5所示，低阶次非常清楚，但是高阶次却模糊不清，这是在做阶次分析时经常会遭遇到的现象。
假设某旋转机械的转速（假设转速变化率固定）以固定速率发生变化，在50s的时间间隔内转速从600rpm上升到6600rpm，那么，转速的变化率是120rpm/s，转频的变化率是2Hz/s。1阶次将以2Hz/s的速率发生变化，第3阶次将以6Hz/s的速率变化，第30阶次将以60Hz/s的速率变化，也就是说阶次越高，频率变化速度越快，正比例于阶次成分。对于旋转轴带有30个齿的齿轮盘而言，就属于这种情况，旋转轴1秒变化2Hz，而齿轮1秒变化60Hz。对于高阶次而言，频率成分是很高的，在同样一个时间长度之内，如果是一个低频信号，可以认为幅值变化不大，但对于一个高频信号，幅值变化是很明显的。除了幅值变化之外，还有频率变化，假设一秒钟之内，低频1阶100Hz变化到102Hz，只有2Hz的差别。但是30阶次，高频3000Hz已变化到3060Hz，这个时候变化的频率有60Hz。在这个时间之内，除了这两个信号之外，还有3000~3060之间的频率成分，因为信号一直在变化，是从3000Hz连续变化到3060Hz，也就是说一秒钟的时域信号里面包含了3000-3060Hz的频率成分，实际上这个信号变化过程中永远只有一个频率，这个频率对应旋转轴转速频率的30倍频。在这个过程中，永远是它的30倍频，只不过从Hz上看是连续变化的，但实际上在任何时候只有一个频率，就是旋转轴转速的30倍频。
由于转速连续变化，30阶次这一秒钟内的频谱从3000Hz连续变化到3060Hz，频谱变成了连续谱，离散的谱线变成了谱带或者说谱线变胖，从而导致高阶次在频域的阶次线变得模糊。这种模糊的阶次尤其针对高阶谐波，带宽按阶次比例改变，谱带更宽，谱图变得模糊不好分辨。这就是为什么阶次分析时，高阶次成分模糊不清的根本原因。特别是转速变化速率越快的情况，这个现象更明显。
这个例子，我们之前介绍过，但介绍的是最基本的情况，在这，我再扩展一下，讲解一些特殊的情况下的阶次成分。带有6块叶片的风扇的主轴阶次是1阶次，叶片的通过阶次6阶次。简单地说，主轴每转一圈，将有6个叶片通过，使得我们可以明白叶片的通过阶次是6阶次。或者说主轴每旋转一圈，在任一角度都可以看到6个叶片通过该位置，因此，叶片通过这个位置每旋转一圈发生6次，对应6阶次。也可以理解成，旋转时，各个叶片的角度差始终是60度的倍数，因此对应6阶次。除了6阶次之外，还会产生谐阶次，即6阶次的倍频，如12，18阶次等。出现6阶次的谐阶次的可能原因是旋转轴不对中，如旋转轴的轨迹是椭圆，这时就容易产生2倍的谐阶次。
更进一步，假设这个风扇还是6个扇叶，每个扇叶形状都相同，但每两个扇叶之间的角度都不相同，这时候产生的阶次噪声1-12阶（连续的整数阶）都有，这怎么理解呢？由于每两个扇叶角度不一样，那么每旋转一圈可能在多个角度位置出现，并且这些角度差都不相同，不是某个角度的倍数，所以确切地说1-6阶次都有。而7-12阶次是它们的谐阶次。如果角度相同，那么旋转一圈，只在6个角度处出现，所以只有6阶次及其谐阶次。假设风扇还是6个扇叶，每个扇叶形状都相同，而且前三个扇叶为第1组，组内每两个叶片之间的角度都不相同；后三个扇叶为第2组，组内每两个叶片之间的角度也不相同，但是第1组和第2组呈中心对称，那么其产生的阶次噪声为2 、4、6、8等连续的偶数阶次。如果扇叶不对称分布，如上面那个情况，则产生连续的整数阶次成分。因此，如果只考虑其中任一组扇叶，将产生连续的整数阶次，但是由于两组成对称分布，所以连续的整数阶次都要乘以2，也就是说1，2，3阶次变成了 2，4，6阶次。故，这种情况下产生的阶次为连续的偶数阶次。
文章转自：模态空间
infinite cui
需求VDA6.3 表格，谢谢
准备与BMW配套？这些要求都知道了吗 – 汽车质量管理笔记
[…] 《看看宝马是怎么培训供应商的~》（点击可查看）。 […]
大师兄
说的挺有道理的，从现实看到的大部分情况，做技术的人都比较直，对技术的一丝不苟，容易在遇到需要展现管理能力的时候，就会表现出短板来。管理需要授权，更多应该思考团队、部门间，人员发展，对未来的变化做出应对等的能力。
john
如何获得这个PPT文件
除尘
文章写的很好，对于摩擦系数测定这些基础知识介绍很详细，是个好读物。
