瀑布图分析注意事项

共计 2445 个字符，预计需要花费 7 分钟才能阅读完成。

瀑布图分析经常用于评估旋转机械噪声和/或振动的表现。这个处理过程要对随转速变化的每个固定长度的子段数据块使用FFT变换计算频谱，转速的变化可能是升速也可能是降速。需要花时间去采集足够的数据以便得到一个时域数据块用于瞬时（单次）FFT计算（实际时域数据块是很短的），而在采集这个数据块的同时，机械设备的转速将从时域数据块采集开始时到结束一直在发生变化。

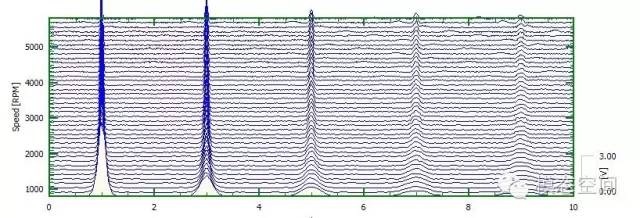
跟踪转速的瀑布图分析仍然采用“跳跃的FFT变换”方式，与跳跃时间（跟踪时间方式）的区别在于，当执行FFT变换时，跳跃的步长为等转速步长，而非等时间步长。以等转速步长计算瞬时FFT频谱，如转速步长为25rpm，则表示转速每变化25rpm，计算一次瞬时频谱，每次FFT变换对应的时域数据长度为频率分辨率的倒数。每个数据块对应一个转速（实际上各个数据块对应的转速一直在变化，软件会按某种算法得到这个数据块对应的转速，如平均转速），然后按照转速的先后顺序将各瞬时频谱排列得到三维瀑布图。而彩图则是用二维图来显示，只不过用颜色深浅来表示幅值大小。在瀑布图或彩图中，频谱并不连续，各频谱之间有间距，间距为等转速步长。在瀑布图中可以看出各频谱有间距，但在彩图中看不出来这种间距。

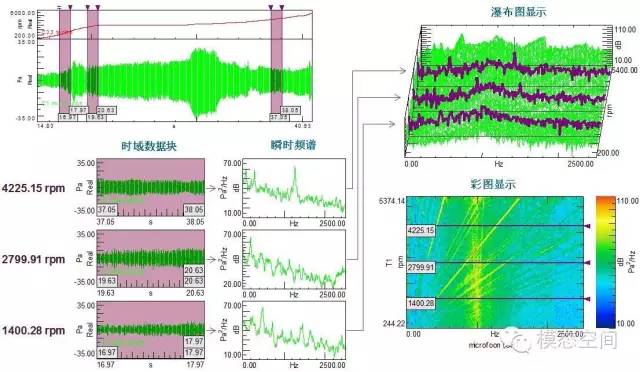
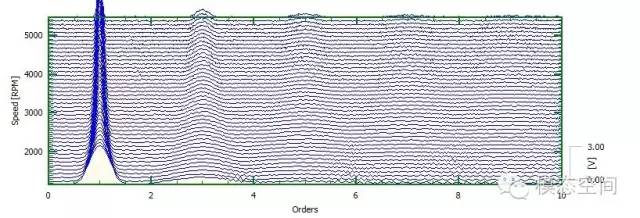
在这以发动机噪声数据为例说明以跟踪转速方式进行瀑布图分析的全过程。图11中左上角为测试的全程时域数据，按等转速步长（跟踪时间则为等时间步长）计算每个固定长度的时域数据块（时间长度为频率分辨率的倒数）得到各数据块对应的瞬时频谱图。然后按照等转速步长的时域数据块先后顺序将所有对应的瞬时FFT进行排列，得到三维瀑布图。从测试的全程时域数据中取3个数据块进行说明，左上角三个阴影区域对应这3个时域数据块。时域数据块长度为1s（频率分辨率为1Hz），计算其相应的瞬时频谱，由于采样频率不变，所以瞬时频谱对应的带宽都相同，这三个数据块对应的瞬时频谱如图8中间所示，对应的转速分别为1400.28，2799.91和4225.15rpm。然后在瀑布图中按转速的先后顺序排列所有的瞬时频谱，图11中选取的3个数据块对应的瞬时频谱在瀑布图或彩图中对应的频谱为图11中右则图中的紫色线条所示。

图11 瀑布图分析全过程示意

在采集每一个数据块的过程中，转速都在变化，因而采集到的时域数据块将会产生一种所谓的数据拖尾现象。在这强调数据产生拖尾现象的原因，以帮助大家明白当采集和分析旋转数据时必须要考虑的因素。

接下来对之前的噪声信号进行瀑布图分析，处理的下一步是再次执行所谓的“跳跃的FFT变换”处理，但这次代替等时间步长FFT计算（图4），而是以等转速步长计算FFT。这个过程就是众所周知的“瀑布图”处理。我们的噪声信号的瀑布图如图12所示。

图12 瀑布图（频率VS转速）

现在我们能清晰地看出与转速相关的噪声的线性特性。这表明在瀑布图中噪声随斜线上升。因为这次的测试对象是一个4缸4冲程发动机，主导频率是曲轴转速的2倍或者2次谐波。在旋转机械中，我们称这个为2阶次。

转速变化速率对瀑布图的影响

频域分析需要考虑的是确定最优的频率分辨率。使用FFT技术进行频谱计算时，要求截取一定长度的时域信号以实现指定的频率分辨率，也就是说实际捕捉的时域信号长度等于分析的频率分辨率的倒数。

譬如：

• 如果你需要1Hz的频率分辨率，那么获得这个频率分辨率所要求捕获的时域数据块的长度为1s。
• 如果你需要2Hz的频率分辨率，那么只需要0.5s的时域数据块。

在采集时域数据块的过程中，待测的旋转机械的转速（假设转速变化率固定）将以固定速度发生变化。如果你在10S的时间间隔内捕获的数据从600rpm上升到6600rpm，那么，转速的变化率将是6000rpm/10s或者是600rpm/s:

• 基础转频（1阶次）将以10Hz/s的速率发生变化。
• 第3阶次将以30Hz/s的速率变化。
• 第5阶次将以50Hz/s的速率变化。

假设你对捕获的数据进行分析，要求满足1Hz的频率分辨率，那么FFT计算信号的第5阶次的能量将会分布在50条谱线上。

出于这个原因，当你发现转速的变化速率越来越快时，那么，你必须关心何时选择怎样的频率分辨率用于分析。

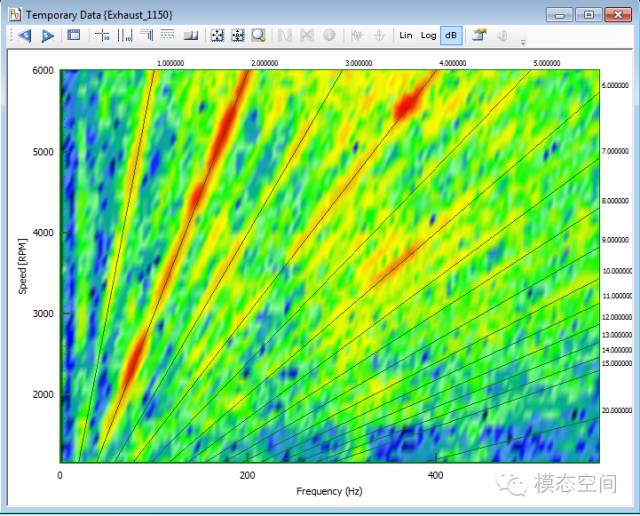
对转速在21s内从840rpm上升到4800rpm的振动信号进行瀑布图分析，此时转速的变化率约为188rpm/s。分别作0.5Hz和5Hz的频率分辨率的瀑布图分析，对应的colormap如图13所示。0.5Hz对应的时域数据块长度为2s，5Hz对应的时域数据块长度为0.2s，从图中可以看出，5Hz的频率分辨率下各阶次更明显，这是因为相应的时域数据块更短，在这个更短的时间内，转速变化没有0.5Hz对应的时域数据块的转速变化大，因此，频率更清楚。时域数据块越短，越可以认为在该时间段内信号是稳态信号。因此，当作瀑布图分析时，需要根据转速的变化速率来选择合适的频率分辨率。更优的频率分辨率（频率间隔越小），频谱拖尾更严重，特别是在转速高的情况下。信号出现“拖尾”现象是因为信号的频率在采集时域数据块的过程中是变化的。当然还有栅栏效应和泄漏的原因。

图13 上图0.5Hz，下图5Hz的频率分辨率

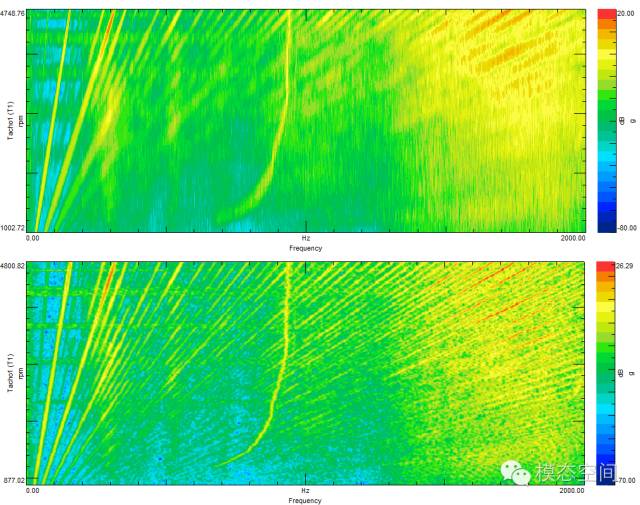
如果你能控制转速变化的速率，那么这总是最合适的测试方式。然而，往往转速变化的时间却总是不确定的，比如汽车测试的特定工况是节气门全开工况（WOT）。图14和15是两种不同升速过程的瀑布图结果。

通过观察第3阶，可以清楚地发现，当转速变化速率越快，频谱对应的能量越“拖尾”严重。观察的阶次越高，转速变化速率越快。转速变化速率越快，阶次越不明显。

图14 1阶次变化的速率等于150rpm/s

图15 1阶次变化的速率等于1200rpm/s

以上的讨论表明转速的变化速率与分析的频率分辨率之间的关系。要在这两个参数之间进行权衡。用户通常想获得高的分辨率（更小的频率间隔），但这要求采集更长的时域数据块用于FFT计算。在采集时域数据块的过程中，转速变化可能非常快，那么，这将导致能量分布到多条、相邻的谱线上，出现拖尾现象。

文章转自：模态空间