共计 2907 个字符，预计需要花费 8 分钟才能阅读完成。
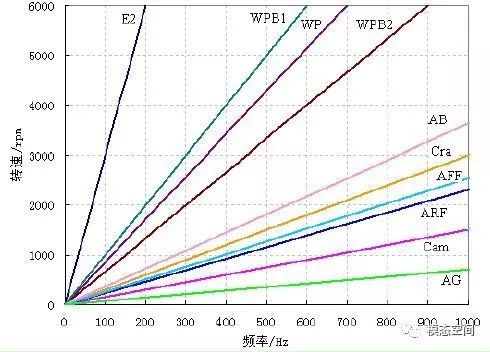
齿轮的特征阶次与齿数相关，在对齿轮进行故障诊断时，根据参与啮合的齿轮对的齿数可以确定故障齿轮所在，从而快速的确定问题齿轮，因此，通常在故障诊断之前应根据传动比来计算各级参与啮合的齿轮的特征阶次。这是因为各级齿轮的齿数是不相同的，那么，对应的阶次也不相同，在进行阶次分析时，根据瀑布图或colormap图中的阶次可以确定NVH发生在哪级齿轮。如图1是发动机各旋转部件与曲轴转速之间的阶次关系图。当实际测试时，如果发现某阶次的响应特别大，就可以通过这个阶次关系确定是发动机哪个部件产生的响应，从而能快速的找到问题所在。
E2：动机二阶激励； Cam：凸轮轴正时齿轮； Cra：曲轴正时齿轮 WP：水泵叶片； WPB1：水泵轴承滚珠； WPB2：水泵轴承滚柱；A：发电机； AFF：发电机前风扇； ARF：发电机后风扇；AB：发电机轴承； AG：发电机线槽
齿轮的传动比定义为主动轮与从动轮角速度（转速）之比，也称为速比。如图2所示的圆柱齿轮副，主动轮和从动的转速分别为n1和n2，齿数分别为z1和z2，则传动比为
式中取负是表示两个齿轮旋转方向相反。通常对于一对齿轮啮合的情况，如果是外啮合，则取负；如果是内啮合，则取正。对于圆锥齿轮传动和蜗杆传动，由于主/从动轮运动不在同一个平面内，则不能用正负号来确定，可以用箭头来表示旋转方向。
对于齿轮齿条传动，若ω1表示齿轮的角速度，d1表示齿轮1分度圆直径，v2表示齿条的移动速度，存在以下传动关系：
如果传动系统是多级定轴齿轮，传动比为首转（输入轮）与末轮（最终输出轮）的角速度之比。此时的传动比在数值上等于组成该定轴齿轮系的各对啮合齿轮传动比的连乘积，也等于首末轮之间各对啮合齿轮中所有从动轮齿数的连乘积与所有主动轮齿数的连乘积之比。 设定轴齿轮系首轮为1轮、末轮为K轮，定轴齿轮系传动比公式为：
i=n1/nk=各对齿轮传动比的连乘积
i1k=(-1)m所有从动轮齿数的连乘积/所有主动轮齿数的连乘积
式中，m表示轮系中外啮合齿轮的对数。当m为奇数时传动比为负，表示首末轮转向相反；当m为偶数时传动比为正，表示首末轮转向相同。
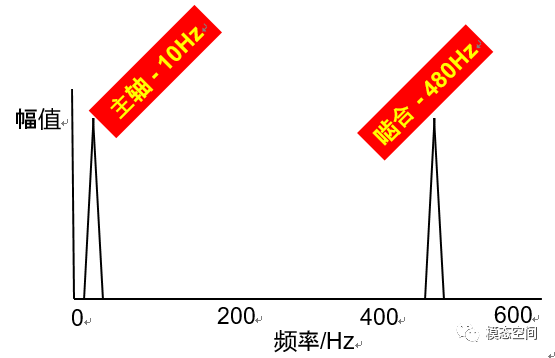
定轴齿轮的转频等于转速除以60，啮合频率等于转频乘以齿数。如图3所示齿轮的齿数为48，假设转速为600rpm，那么它的主轴转频为10Hz，啮合频率等于480Hz，也就是一秒钟内齿轮要啮合480次，频率如图4所示。那么，它的阶次是多少呢？
在《怎么理解阶次》一文中，我们已经说明：频率是一秒钟内事件（振动或噪声）发生的次数；阶次是旋转一圈内事件发生的次数。而转速是每分钟转动的圈数，转频为每秒钟转动的圈数，因此，一秒钟内阶次对应的事件发生的次数等于每秒转动的圈数乘以一圈事件发生的次数，即等于转频乘以阶次。也就是说，阶次等于一秒钟内事件的频率除以转频。因此，图2所示的齿轮的阶次等于啮合频率除以转频，等于齿数，即48阶次，这也表明这个齿轮旋转一圈要啮合48次。
通常以输入轴的转频或转速作为参考来计算阶次，也就是把输入轴的阶次作为参考阶次，那么，各个齿轮的阶次等于它所在轴的阶次乘以齿数。以输入轴的转速为参考时，齿轮所在轴的阶次等于传动比，这就是为什么在计算阶次之前应该计算参与啮合的各级齿数的传动比的原因所在。此时，齿数的阶次为
如果我们认为齿轮所在轴的转频为1阶次，那么齿轮的阶次等于齿数。之前在《怎么理解阶次》一文中提到过，如果以不同的轴作为参考，那么同一齿轮的阶次是不同的，因为参考的轴不同，二者相差的倍数即为二者的传动比。在一对齿轮幅中，两个啮合的齿轮的啮合频率是相等的，同样的道理，两个啮合的齿轮的阶次也是相等的。
由于行星齿轮的行星轮既自转又公转，因此，肯定不能直接使用定轴齿轮系的传动比计算公式来计算行星齿轮的传动比。在《行星齿轮的特征频率》一文中已说明需要转化，当时是以行星架的转速作为参考，其他轮的转速均相对于行星架来计算相应的特征频率。这样可以认为行星架的转速为0，在这里仍然是采用这个思路，只是稍有不同（实旨是一样的），我们需要给行星架加上一个与行星架的转速大小相等，但转向相反的转速nH。根据相对性原理，此时整个行星轮系的各个构件间相对运动关系不变。但行星架的转速为0，即原来旋转的行星架转化为静止。这样一来，行星齿轮系就转化为定轴齿轮系，从而可以使用定轴齿轮系的啮合频率公式来计算传动比了。
假设行星齿轮系的各个构件的相应参数如表1所示，在这考虑的行星齿轮系各个构件的轴线位于同一条直线上。同时定义齿圈与太阳轮的齿数比为a，即
表1 行星齿轮系的各个参数
| 构件 |
转速 |
相对转速 |
齿数 |
数量 |
| 齿圈 |
n1 |
n1-nH |
z1 |
1 |
| 太阳轮 |
n2 |
n2-nH |
z2 |
1 |
| 行星轮 |
n3 |
n3-nH |
z3 |
n |
| 行星架 |
nH |
0 |
|
1 |
现在假设齿圈固定，太阳轮作为主动轮，行星架作为从动轮。此种情况下齿圈的实际转速n1=0，但由于假定行星架相对转速为0，齿圈的相对转速大小为nH，由于行星轮此时作为中间轮，不影响啮合频率，根据定轴齿轮的啮合频率计算公式有（式中略去了除以60，以下相同）
第二种情况是假设太阳轮固定，行星架作为主动轮，齿圈作为从动轮。此种情况下太阳轮的实际转速n2=0，由于假定行星架转速为0，太阳轮的相对转速大小为nH，由于行星轮此时作为中间轮，不影响啮合频率，根据啮合频率计算公式有
i= nH/n1=z1/(z1+z2)=a/(1+a)
第三种情况是假设行星架固定，太阳轮作为主动轮，齿圈作为从动轮。这种情况下行星架固定，则传动比计算公式为
第四种情况是联锁三个基本构件中的任意两个，则传动比恒为1。
将上述四种情况的单排单级行星齿轮的传动比总结如表2所示。
表2 单排单级行星齿轮的传动比
| No. |
固定 |
主动轮 |
从动轮 |
传动比 |
| 1 |
齿圈 |
太阳轮 |
行星架 |
1+a |
| 2 |
太阳轮 |
行星架 |
齿圈 |
a/(1+a) |
| 3 |
行星架 |
太阳轮 |
齿圈 |
a |
| 4 |
联锁任意两个构件 |
1 |
在《行星齿轮的特征频率》一文中，我们总结过一个计算啮合频率的简单算法：只要行星架转动，相应的啮合频率就是行星架转速*固定的那个齿轮的齿数/60。在这，我们假设主动轮的转速为1阶次来计算各种情况下的啮合阶次。对于表2中的第一种情况，啮合频率为nHz1，而传动比为1+a，所以这种情况下的啮合阶次为z1/(1+a)。对于第二种情况，啮合频率为nHz2，而行星架作为主动轮，那么它的啮合阶次为z2。第三种情况是行星架固定，则相当于定轴齿轮，因而啮合阶次为主动轮的齿数z2。上述情况的啮合阶次如表3所示。
表3 单排单级行星齿轮的啮合阶次
| No. |
固定 |
主动轮 |
从动轮 |
啮合阶次 |
| 1 |
齿圈 |
太阳轮 |
行星架 |
z1/(1+a) |
| 2 |
太阳轮 |
行星架 |
齿圈 |
z2 |
| 3 |
行星架 |
太阳轮 |
齿圈 |
z2 |
文章转自：模态空间
透彻理解卡方检验 - 汽车质量管理笔记
[…] 化简后的式子是我们在卡方检验中需要用到的式子，所以请大家牢记！对于上述式子有疑惑的读者可以学习基础的概率论，也可以参考我之前写的一篇关于独立的文章（《【直观数学】如何理解两事件间的独立关系》）。如果没有问题的话，我们可以进入到卡方检验原理与步骤的主体介绍部分！ […]
infinite cui
需求VDA6.3 表格，谢谢
大师兄
说的挺有道理的，从现实看到的大部分情况，做技术的人都比较直，对技术的一丝不苟，容易在遇到需要展现管理能力的时候，就会表现出短板来。管理需要授权，更多应该思考团队、部门间，人员发展，对未来的变化做出应对等的能力。
john
如何获得这个PPT文件